- #1
airborne18
- 22
- 0
Homework Statement
I don't know why but my brain is having one of its moments and I can't work through this. Not even on paper anymore.
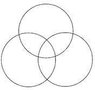
Okay so I have 3 intersecting circles. Like a Venn Diagram. How do I find the area of all three minus the instersecting parts. I know how to do two intersecting, but I am trying to break this down into an algorithm to process it in my brain.
This is not homework, but I am posting it here. I just need some help with sequencing the steps to solve it, and then my brain might click with again. I am mentally stuck with the application so need a kick start.