- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hello! (Wave)
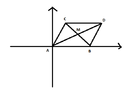
Suppose that a parallelogram $ABCD$ has vertices $A=(0,0)$ and $B=(1,0)$. In terms of $C=(x,y)$, find the position of $D$ and where the two diagonals will intersect.
Then we will have something like that:
View attachment 5378How can we find the coordinates of $M$, i.e. the point at which the two diagonals intersect?
Suppose that a parallelogram $ABCD$ has vertices $A=(0,0)$ and $B=(1,0)$. In terms of $C=(x,y)$, find the position of $D$ and where the two diagonals will intersect.
Then we will have something like that:
View attachment 5378How can we find the coordinates of $M$, i.e. the point at which the two diagonals intersect?