- #1
etf
- 179
- 2
Hi!
My task is to find discrete signal x(n), if z transform of that signal is $$X(z)=\frac{5}{(z-2)^{2}}$$. It is known that signal is causal. Here is what I have done. Since signal x(n) is causal, convergence of z transform of that signal will be outside of circle with radius r:
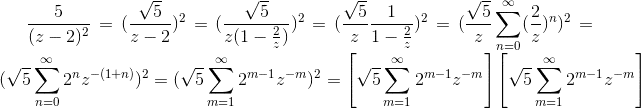 We have in bracket sum which represents z transform of signal:
We have in bracket sum which represents z transform of signal:
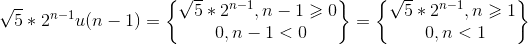
But I don't know what to do next :(
My task is to find discrete signal x(n), if z transform of that signal is $$X(z)=\frac{5}{(z-2)^{2}}$$. It is known that signal is causal. Here is what I have done. Since signal x(n) is causal, convergence of z transform of that signal will be outside of circle with radius r:
But I don't know what to do next :(
Last edited: