Is My Understanding of the Generalized Stokes' Theorem Correct?

  • I
  • Thread starter davidge
  • Start date
In summary, asking "Is my understanding correct?" is a way to confirm the accuracy of one's understanding of a topic or concept. To determine if it is correct, seeking feedback from others or doing further research is recommended. It is crucial to have a correct understanding in the scientific field to ensure validity and reliability in research and experiments. If one's understanding is incorrect, it is important to correct it as soon as possible by seeking guidance or researching reliable sources. Over time, one's understanding may change as new information and research becomes available, emphasizing the importance of continuous learning in the scientific field.
  • #1
davidge
554
21
I was interested in finding a motivation for the generalized Stokes' theorem. I was asking myself why
$$ \int_D d \omega = \int_{\partial D} \omega $$ for a region ##D## and a (p-1)-dimensional form ##\omega##.
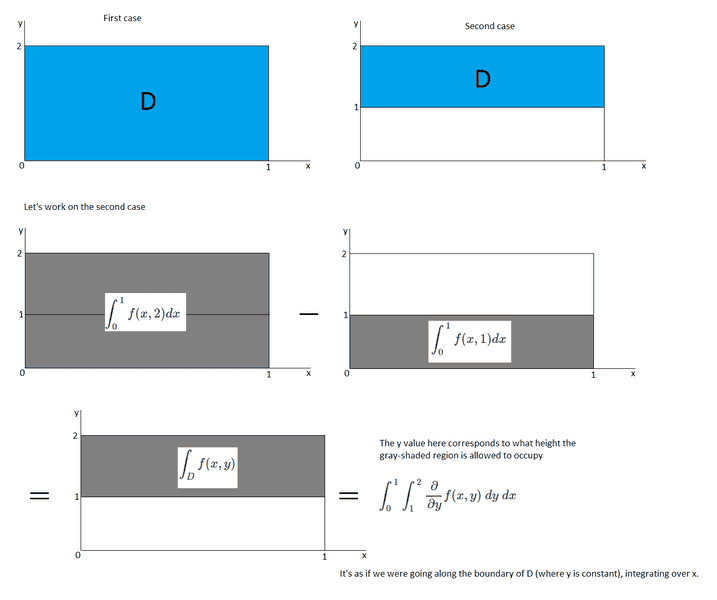
Then I found something funny when working with some arbitrary functions in two dimensions. Below is what I found.
In the second image, I called ##x^{\mu}_{i}## and ##x^{\mu}_{f}## the coordinates of the initial and final points, respectively.
My question is: Is this actually correct?

kLxFrqv.png

OTrcGLW.png
 
Physics news on Phys.org
  • #2
I'm not sure about that generalization from 2 to p dimensions that I did above.
 

1. What is the purpose of asking "Is my understanding correct?"

Asking "Is my understanding correct?" is a way to confirm if your understanding of a certain topic or concept is accurate. It is a common question that arises when learning something new or trying to gain a deeper understanding of a subject.

2. How can I determine if my understanding is correct?

To determine if your understanding is correct, you can seek feedback from others who are knowledgeable on the topic or do further research to verify your understanding. It is also helpful to ask clarifying questions to ensure a complete understanding.

3. Is it important to have a correct understanding?

Yes, having a correct understanding is crucial in the scientific field. It allows for accurate and reliable research and experiments to be conducted, leading to valid conclusions and advancements in the field.

4. What should I do if my understanding is incorrect?

If you discover that your understanding is incorrect, it is important to correct it as soon as possible. This can be done by seeking guidance from a mentor or researching reliable sources to gain a better understanding.

5. Can my understanding change over time?

Yes, it is possible for your understanding to change over time as new information and research emerges. This is why it is important to continually learn and stay updated in the scientific field.

Similar threads

I Resources on the Derivation of generalized Stokes' theorem
    • Differential Geometry
Replies
11
Views
386
I Understanding De Rham's Period and Stokes Theorem
    • Differential Geometry
Replies
5
Views
1K
I Proving Stokes' Theorem: General Cases and the Fundamental Theorem of Calculus
    • Differential Geometry
Replies
9
Views
3K
I Vector valued integrals in the theory of differential forms
    • Differential Geometry
Replies
4
Views
2K
I Calculating the Hodge Star in the most general case
    • Differential Geometry
Replies
29
Views
1K
A Non-Abelian Stokes theorem and variation of the EL action
    • Differential Geometry
Replies
4
Views
2K
I Diffeomorphism invariance and contracted Bianchi identity
    • Differential Geometry
Replies
7
Views
3K
Understanding the math of definition of electromotive force
    • Introductory Physics Homework Help
Replies
1
Views
105
I Alternate forms of Stokes' theorem? Are they correct? Are they named?
    • Calculus
Replies
2
Views
1K
Finding the Wrong Answer with Stokes' Theorem
    • Calculus and Beyond Homework Help
Replies
4
Views
806

Hot Threads

Recent Insights

Back
Top