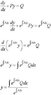Is there an easy trick to this (getting into form)

[amb123]

I am trying to solve a linear 1st order diff eq. I have found the integrating factor, and multiplied it through the equation, now expecting it to be exact. However, I can't get it into an easy to solve form.
After multiplying by the integrating factor I have :

(e^-3x) dy/dx - (3e^-3x) y = 6e^-3x I can't figure out how to get this into form. The schaum's book puts this in the form d/dx [ye^-3x)] = 6e^-3x. I see that if you use the product rule on ye^-3x you get the original, but I'm not sure how you figure out how to get the original to the second form. Is there a trick? Can my TI89 do it? Any help is greatly appreciated. I have a test tomorrow and I'm not doing terribly well. I understand the problem before and after this part, but not this transition.

thx.
-A

 

[Zurtex]

1st order linear differential equations are quite simple. First you must get it into this form:

$$\frac{dy}{dx} + Py = Q$$

Where P and Q are functions of x or constants. Next work out:

$$e^{\int P dx}$$

Multiply your whole equation by that to get:

$$e^{\int P dx} \frac{dy}{dx} + e^{\int P dx}Py = e^{\int P dx}Q$$

Notice that the left hand side takes the form of the product rule, so we can now get:

$$\frac{d}{dx} \left( e^{\int P dx} y \right) = e^{\int P dx}Q$$

$$e^{\int P dx} y = \int e^{\int P dx}Q dx$$

$$y = \frac{\int e^{\int P dx}Q dx}{e^{\int P dx}}$$

 

[amb123]

How do I read your boxed text, is there a program I need to d/l?

thx.
a

 

[Zurtex]

How do I read your boxed text, is there a program I need to d/l?

thx.
a

No, it is just supposed to display the appropriate maths symbols, I'll PM a mod and ask what went wrong.

 

[A_I_]

i don't know i guess, if he's in a hurry,
he can click and it opens a link with html langage
but easily understood equations :)

 

[Zurtex]

Sorry, I've been told the LaTeX interpreter was down yesterday and LaTeX still doesn't seem to be working, so I've typed it up on my computer and saved it as a JPEG file.

Just a little explanation:

1st line: P and Q are functions of x or constants

2nd line: Multiplying the whole thing by e^(Integral of P with respect to x). Notice now the left hand side takes the form of the product rule.

3rd line: Putting in the form d/dx (uv)

4th line: Integrating both sides

 

[amb123]

It's the second to third line that I'm not seeing here. How do you know what is d/dx(uv) ? I can see it going backward, that using the product rule on uv gives the previous line, but I can't see it going forward. How do you know what is u and v from looking at eq 2?

Thanks for taking the time to help!
-A

 

[JonF]

With out being able to see the latex I am not sure if I am answering your question.

But what the integrating factor you used is put something in the form of:

y` * f(x) + f’(x) * y =
where f(x) is your integrating factor

but y` * f(x) + f’(x) * y is the product rule backwards

that means: y’ * f(x) + f’(x) * y = d(f(x)*y)/dx.

So you can integrate each side of the equation to remove your differentiation around the f(x)*y.

Which gives you f(x)*y. now of course what ever you do to one side of the equation you need to do to the other, so you will multiply the rhs by your integrating factor and then integrate it.

 

[Zurtex]

JonF I posted up a image of the workings in a later post.

Sorry LaTeX still doesn't seem to be working but I'll try and make myself as clear as possible.

The first thing we know is that d(y)/dx = dy/dx. So we can say that u = y and u'=dy/dx

If we look at the left hand side of line 1 this gives us:

u' + Pu

Where P is some function of x. If we now multiply the whole thing by another function of x we get:

f(x)u' + f(x)Pu

Now as the standard form of the product rule is: vu' + v'u = d(uv)/dx

Comparing we can say that v = f(x) and v'=f(x)P

If we let f(x) = e^(Integral of P dx) this gives us f'(x) = [e^(Integral of P dx)]P = f(x)P

So with f(x) = e^(Integral of P dx) we now have the form:

vu' + v'u

We can now let this equal d(uv)/dx



Hope that helps.




Edit: My 1st post is now working