- #1
- 1,752
- 143
Kirchoff's Rules
I can not find a good explanation anywhere for Kirchoff's rules. Googling onlygives me links that don't explain it well, and my textbook's explanation is lacking as well. I'll go over my textbook's description, so hopefully someone here can clarify this for me.
1. Identify any series or parallel combinations and find the simplest equivalent circuit. (easy to do)
2. Define a current variable and choose a positive sense for each variable. The direction you label need not be the actual direction of the current.
WHY? If I get the direction wrong, I'll be adding where I should be subtracting, and that'll give me the wrong answer. Every link says this too, but none of them explain it.
3. Use symmetry if possible to reduce the number of independent variables.
What does this mean? What is an independent variable anyway? What would be an example of a dependent variable?
4. Write junction equations until each current appears in at least one equation.
What is a junction equation? I hate my textbook for using terms it doesn't define. Do they mean I1+I2=I3?
5. Write loop equations until each arm of the circuit occurs in at least one of the loops.
What is a loop equation? Do they mean I=V/R
6. Solve for unknowns
Unknown is how to use Kirchoff's rules
So, for example, how would I do this problem:
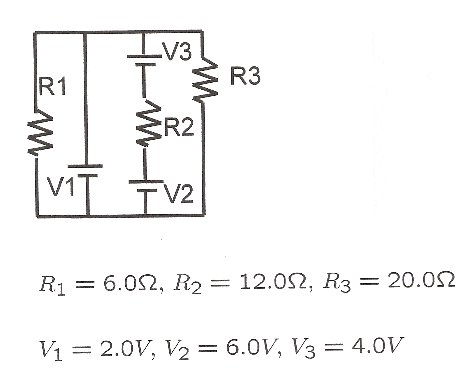
I can not find a good explanation anywhere for Kirchoff's rules. Googling onlygives me links that don't explain it well, and my textbook's explanation is lacking as well. I'll go over my textbook's description, so hopefully someone here can clarify this for me.
1. Identify any series or parallel combinations and find the simplest equivalent circuit. (easy to do)
2. Define a current variable and choose a positive sense for each variable. The direction you label need not be the actual direction of the current.
WHY? If I get the direction wrong, I'll be adding where I should be subtracting, and that'll give me the wrong answer. Every link says this too, but none of them explain it.
3. Use symmetry if possible to reduce the number of independent variables.
What does this mean? What is an independent variable anyway? What would be an example of a dependent variable?
4. Write junction equations until each current appears in at least one equation.
What is a junction equation? I hate my textbook for using terms it doesn't define. Do they mean I1+I2=I3?
5. Write loop equations until each arm of the circuit occurs in at least one of the loops.
What is a loop equation? Do they mean I=V/R
6. Solve for unknowns
Unknown is how to use Kirchoff's rules
So, for example, how would I do this problem: