- #1
- 3,486
- 257
Edit: I think I may have found my problem. See my second post below.
I'm trying to solve this problem from Kleppner and Kolenkow:
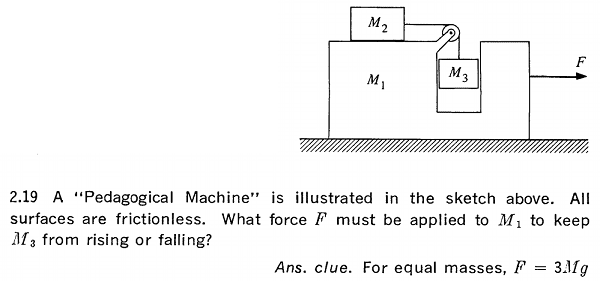
But I seem to be missing something because my answer doesn't match the clue. I have worked out the entire problem but I want to focus on the physical content so I'll just show my force equations below. I think the mistake is with one of them because I've checked my algebra in the rest of the problem several times.
##F=ma##
I chose coordinates ##x## pointing to the right and ##y## pointing upward, stationary relative to all of the masses.
Mass 2 - vertical forces
We have an upward normal force of ##N_2## and a downward weight of ##M_2 g##. This mass does not accelerate vertically, so ##N_2 = M_2 g##.
Mass 2 - horizontal forces
The only horizontal force on ##M_2## is the tension in the rope. I call it ##T##. It is pointing to the right and satisfies ##T = M_2 \ddot x_2##.
Mass 3 - vertical forces
This mass is acted upon by the same tension ##T## in the upward direction, and weight ##M_3 g## in the downward direction. Thus, ##T - M_3 g = M_3 \ddot y_3##.
Mass 3 - horizontal forces
I assume mass 3 is touching the walls of the slot in which it is situated, so there are normal forces from each wall. I denote these by ##N_3## pointing rightward and ##N_4## pointing leftward. Thus, ##N_3 - N_4 = M_3 \ddot x_3##.
Mass 1 - vertical forces
Mass 1 is acted upon by downward weight ##M_1 g##, and upward by the normal force exerted by the floor, ##N_1##. It is also acted upon by the downward normal force ##N_2## due to the weight of mass 2. Thus, ##N_1 - N_2 - M_1 g = 0##, where the right hand side is zero because mass 1 is not moving vertically.
Mass 2 - horizontal forces
Mass 1 is acted upon horizontally by the applied force ##F## in the rightward direction. It is also acted upon by the same normal forces as mass 3, but in the opposite directions, so ##N_3## points leftward and ##N_4## points rightward. Thus, ##F + N_4 - N_3 = M_1 \ddot x_1##.
Constraints
Note that mass 3 is constrained horizontally so that it moves in lockstep with mass 1, so ##\ddot x_3 = \ddot x_1##.
Also, the rope connecting masses 2 and 3 causes them to move in lockstep. The horizontal motion of mass 2 relative to mass 1 must match the vertical motion of mass 3. Thus, ##\ddot x_2 - \ddot x_1 = -\ddot y_3##.
Concerns
As I mentioned, if I work out the problem to completion, my answer does not match that of the clue. Moreover, I think the error is conceptual, not algebraic. For suppose I combine the Mass 3 Horizontal equation with the Mass 2 Horizontal equation:
$$N_3 - N_4 = M_3 \ddot x_3$$
$$F + N_4 - N_3 = M_1 \ddot x_1$$
Add these together to obtain
$$F = M_1 \ddot x_1 + M_3 \ddot x_3$$
As noted above, we have the constraint ##\ddot x_1 = \ddot x_3##, so this reduces to
$$F = (M_1 + M_3) \ddot x_1$$
This seems wrong, because the total mass in the system is ##M_1 + M_2 + M_3## and surely ##F## must push all three of these in order to accelerate mass 1. So I think this should be ##F = (M_1 + M_2 + M_3) \ddot x_1##. But I can't see the where my error is.
Homework Statement
I'm trying to solve this problem from Kleppner and Kolenkow:
But I seem to be missing something because my answer doesn't match the clue. I have worked out the entire problem but I want to focus on the physical content so I'll just show my force equations below. I think the mistake is with one of them because I've checked my algebra in the rest of the problem several times.
Homework Equations
##F=ma##
The Attempt at a Solution
I chose coordinates ##x## pointing to the right and ##y## pointing upward, stationary relative to all of the masses.
Mass 2 - vertical forces
We have an upward normal force of ##N_2## and a downward weight of ##M_2 g##. This mass does not accelerate vertically, so ##N_2 = M_2 g##.
Mass 2 - horizontal forces
The only horizontal force on ##M_2## is the tension in the rope. I call it ##T##. It is pointing to the right and satisfies ##T = M_2 \ddot x_2##.
Mass 3 - vertical forces
This mass is acted upon by the same tension ##T## in the upward direction, and weight ##M_3 g## in the downward direction. Thus, ##T - M_3 g = M_3 \ddot y_3##.
Mass 3 - horizontal forces
I assume mass 3 is touching the walls of the slot in which it is situated, so there are normal forces from each wall. I denote these by ##N_3## pointing rightward and ##N_4## pointing leftward. Thus, ##N_3 - N_4 = M_3 \ddot x_3##.
Mass 1 - vertical forces
Mass 1 is acted upon by downward weight ##M_1 g##, and upward by the normal force exerted by the floor, ##N_1##. It is also acted upon by the downward normal force ##N_2## due to the weight of mass 2. Thus, ##N_1 - N_2 - M_1 g = 0##, where the right hand side is zero because mass 1 is not moving vertically.
Mass 2 - horizontal forces
Mass 1 is acted upon horizontally by the applied force ##F## in the rightward direction. It is also acted upon by the same normal forces as mass 3, but in the opposite directions, so ##N_3## points leftward and ##N_4## points rightward. Thus, ##F + N_4 - N_3 = M_1 \ddot x_1##.
Constraints
Note that mass 3 is constrained horizontally so that it moves in lockstep with mass 1, so ##\ddot x_3 = \ddot x_1##.
Also, the rope connecting masses 2 and 3 causes them to move in lockstep. The horizontal motion of mass 2 relative to mass 1 must match the vertical motion of mass 3. Thus, ##\ddot x_2 - \ddot x_1 = -\ddot y_3##.
Concerns
As I mentioned, if I work out the problem to completion, my answer does not match that of the clue. Moreover, I think the error is conceptual, not algebraic. For suppose I combine the Mass 3 Horizontal equation with the Mass 2 Horizontal equation:
$$N_3 - N_4 = M_3 \ddot x_3$$
$$F + N_4 - N_3 = M_1 \ddot x_1$$
Add these together to obtain
$$F = M_1 \ddot x_1 + M_3 \ddot x_3$$
As noted above, we have the constraint ##\ddot x_1 = \ddot x_3##, so this reduces to
$$F = (M_1 + M_3) \ddot x_1$$
This seems wrong, because the total mass in the system is ##M_1 + M_2 + M_3## and surely ##F## must push all three of these in order to accelerate mass 1. So I think this should be ##F = (M_1 + M_2 + M_3) \ddot x_1##. But I can't see the where my error is.
Last edited: