- #1
Zacku
- 65
- 0
Hello everyone,
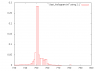
I explain my problem: I have a set of histograms that do not appear normal (in the sense of the normal distribution). I need to convince a referee that it is in fact not normal. I have checked the skewness and the kurtosis and the former is at -2 and the latter is 60 !
I know these values seem non usual but I really double checked and I didn't make any mistake in the calculation of the third and fourth moments.
I would like to know if such a high value for the kurtosis is possible if the histogram is obviously non gaussian.
Just to give you an idea, I join a typical histogram that returns me these crazy values.
Thanks for any comment you would have.
Zacku
I explain my problem: I have a set of histograms that do not appear normal (in the sense of the normal distribution). I need to convince a referee that it is in fact not normal. I have checked the skewness and the kurtosis and the former is at -2 and the latter is 60 !
I know these values seem non usual but I really double checked and I didn't make any mistake in the calculation of the third and fourth moments.
I would like to know if such a high value for the kurtosis is possible if the histogram is obviously non gaussian.
Just to give you an idea, I join a typical histogram that returns me these crazy values.
Thanks for any comment you would have.
Zacku