- #1
willydavidjr
- 66
- 0
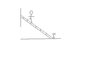
A uniform ladder with a mass of 10 kg leans against a vertical, smooth
wall making an angle of 60 degrees with a smooth floor as shown in
diagram ( I provided the website:
www.geocities.com/willydavidjr/ladder.html ) A nail in the floor keeps
the ladder from slipping while a man (mass = 80 kg) climbs
three-quarters of the way to the top. THe frictional force of the head
of the nail (i.e. the section above the floor) is negligible.
Let the gravitational acceleration be 10 m/s^2 and the value of
squareroot of 3 = 1.73.
a.) Calculate the magnitude of the force exerted on the wall.
b.) Calculate the magnitude of the force exerted on the smooth floor.
c.) Calculate the magnitude of the horizontal force exerted on the
nail.
My work: I am really confused with this problem. First I tried the summation of torque be equal to zero, but the problem is, I don't know the height of the wall where the ladder is leaning, and the ladder itself has no distance. What is the connection of the man climbing 3/4 up to the ladder. Please help me and give me advice with these.
wall making an angle of 60 degrees with a smooth floor as shown in
diagram ( I provided the website:
www.geocities.com/willydavidjr/ladder.html ) A nail in the floor keeps
the ladder from slipping while a man (mass = 80 kg) climbs
three-quarters of the way to the top. THe frictional force of the head
of the nail (i.e. the section above the floor) is negligible.
Let the gravitational acceleration be 10 m/s^2 and the value of
squareroot of 3 = 1.73.
a.) Calculate the magnitude of the force exerted on the wall.
b.) Calculate the magnitude of the force exerted on the smooth floor.
c.) Calculate the magnitude of the horizontal force exerted on the
nail.
My work: I am really confused with this problem. First I tried the summation of torque be equal to zero, but the problem is, I don't know the height of the wall where the ladder is leaning, and the ladder itself has no distance. What is the connection of the man climbing 3/4 up to the ladder. Please help me and give me advice with these.