- #1
Abhishek11235
- 175
- 39
Moved from a technical forum, so homework template missing
Q)6.10 in Morin's Classical Mechanic. All that I have to do is find Lagrangian here. After that only simple motion.
Finding Lagrangian:
Choose the coordinate system at the centre of hoop as shown in 2nd attachment. Then,I found out Lagrangian of the system. Invoking E-L Equations to find the equation of motion, I got equation like shown in 2nd attachment. After solving,I found out equillarabium point i.e ##\ddot \theta## =0. Then ,to find the motion about this point substitute $$\theta \arrow \theta_{0} +\delta$$ and I got equation like in 3rd attachment. Clearly this is not simple harmonic and I gave up.
So,I found out solution through my friend. He got simple harmonic motion by taking angle measuring from downwards verticle. So the change was just cos##\theta## appearance in third term and everything was same.
So my question: Why by choosing ##\theta## measuring from horizontal gives different result when measured from vertical?


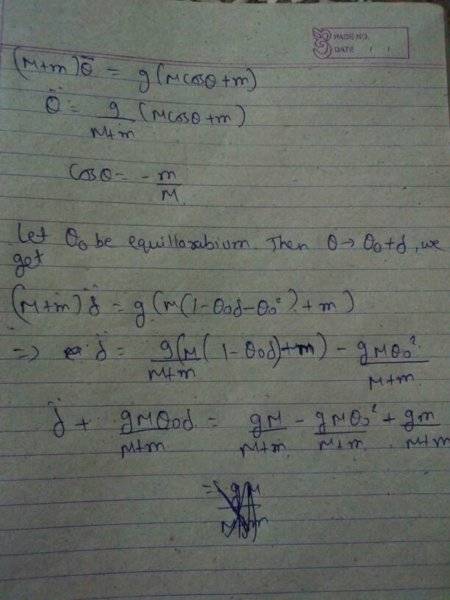
Finding Lagrangian:
Choose the coordinate system at the centre of hoop as shown in 2nd attachment. Then,I found out Lagrangian of the system. Invoking E-L Equations to find the equation of motion, I got equation like shown in 2nd attachment. After solving,I found out equillarabium point i.e ##\ddot \theta## =0. Then ,to find the motion about this point substitute $$\theta \arrow \theta_{0} +\delta$$ and I got equation like in 3rd attachment. Clearly this is not simple harmonic and I gave up.
So,I found out solution through my friend. He got simple harmonic motion by taking angle measuring from downwards verticle. So the change was just cos##\theta## appearance in third term and everything was same.
So my question: Why by choosing ##\theta## measuring from horizontal gives different result when measured from vertical?

