- #1
Messenger
- 68
- 0
I am researching a hypothesis and looking for anyone who is familiar with differential topology (specifically Einstein manifolds). I have access to the Besse book Einstein Manifolds but am also looking for any open questions in differential topology that I am not aware of. I am attempting to develop a solid proof link between the Laplacian and Einstein manifolds (listed in the book as not found yet, free meal up for grabs!). I have seen somewhere that there is a discrepancy concerning the physical representation of Minkowski space, but there were no details listed and can't find the reference anymore. If anyone happens to know a paper detailing this it would be appreciated.
The math is pretty basic, sort of a gauge theory of the Laplacian. In graphical form (as the equations might be confusing without them). So whether function goes to all zero scalars or some arbitrary scalar values will give the same Laplacian [itex]\nabla^2(C-f)=\nabla^2\Phi=0[/itex]
Attempting to equate this to [itex]4\Lambda-R=0[/itex]
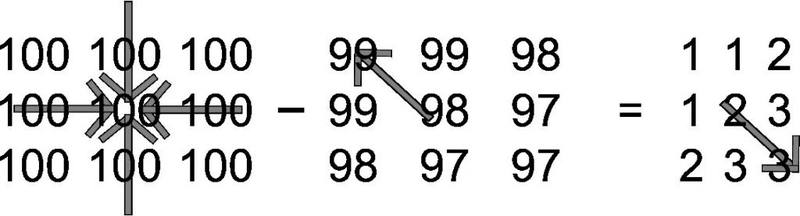
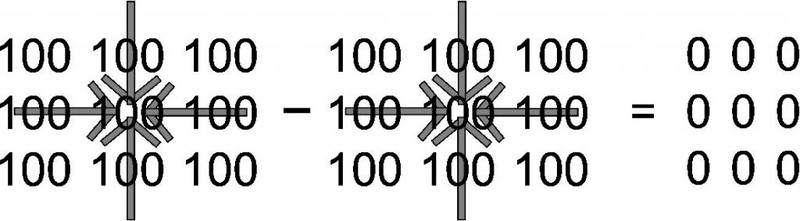
If we flip the integrable function f about the x axis, there is no distinction between the derivatives of the following plots:
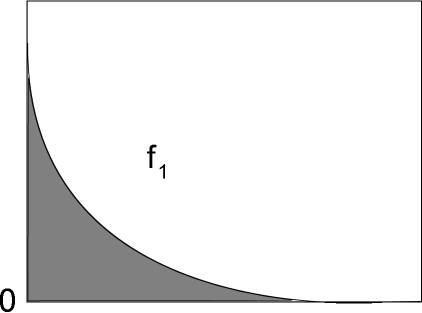
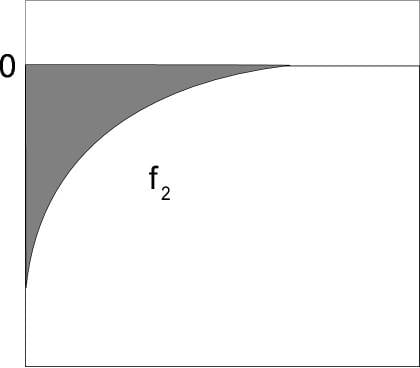
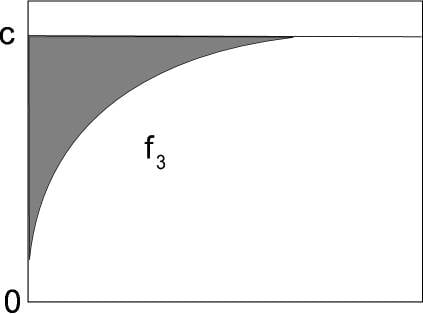
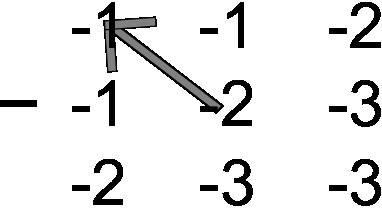
so for two dimensional gradients easier to see:
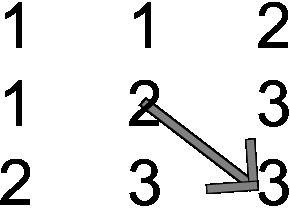
The math is pretty basic, sort of a gauge theory of the Laplacian. In graphical form (as the equations might be confusing without them). So whether function goes to all zero scalars or some arbitrary scalar values will give the same Laplacian [itex]\nabla^2(C-f)=\nabla^2\Phi=0[/itex]
Attempting to equate this to [itex]4\Lambda-R=0[/itex]
If we flip the integrable function f about the x axis, there is no distinction between the derivatives of the following plots:
so for two dimensional gradients easier to see: