- #1
- 3,621
- 1,502
Trying to derive the length of a spring hanging under its own weight. I was trying to approach it like a series of small springs free length ##l## connected in series, in hope to use a limit as ##l \to 0 ## to get the final result, but either I'm bungling it, or it just doesn't work.
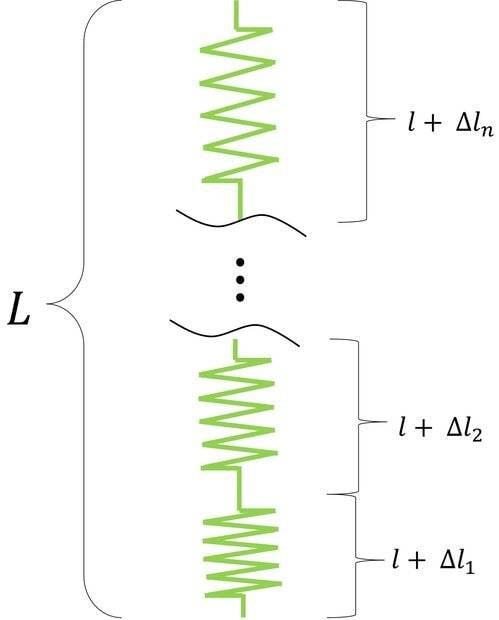
I'm proposing that the total length ##L## is given by:
$$ L = \left( l + \Delta l_1 \right) + l + \left(\Delta l_2 \right) + \cdots + \left( l + \Delta l_n \right) $$
And the force balance on each spring yields:
$$ \Delta l_n = \left( n-1\right)\frac{mg}{k} $$
Where:
## n ## is the number of springs in series
## m ## is the mass of each spring
##k## is the spring constant
So it seems like:
$$ L = ln + \frac{mg}{k}\sum\left(n-1\right) = ln + \frac{n m g}{2 k} \left( n-1\right) $$
I do the following substitutions:
##L_o = l n## The initial free length of the system of springs.
##m = \frac{M}{n} ## ##M## is the total mass if the spring system.
I'm left with:
$$ L_o + \frac{Mg}{2k} \left( n-1\right) $$
This is where I have an ""uh-oh" moment (perhaps I should have had it sooner)?
Any help correcting my course is greatly appreciated.
I'm proposing that the total length ##L## is given by:
$$ L = \left( l + \Delta l_1 \right) + l + \left(\Delta l_2 \right) + \cdots + \left( l + \Delta l_n \right) $$
And the force balance on each spring yields:
$$ \Delta l_n = \left( n-1\right)\frac{mg}{k} $$
Where:
## n ## is the number of springs in series
## m ## is the mass of each spring
##k## is the spring constant
So it seems like:
$$ L = ln + \frac{mg}{k}\sum\left(n-1\right) = ln + \frac{n m g}{2 k} \left( n-1\right) $$
I do the following substitutions:
##L_o = l n## The initial free length of the system of springs.
##m = \frac{M}{n} ## ##M## is the total mass if the spring system.
I'm left with:
$$ L_o + \frac{Mg}{2k} \left( n-1\right) $$
This is where I have an ""uh-oh" moment (perhaps I should have had it sooner)?
Any help correcting my course is greatly appreciated.
Last edited:

