- #1
Tekneek
- 70
- 0
Why is the limit not just infinity?
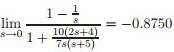
wouldn't it be (1-infinity)/(1+infinity)?
wouldn't it be (1-infinity)/(1+infinity)?
mfb said:Why should "-infinity/infinity" be infinity?
What is the limit of
$$\lim_{s \to 0} \frac{\frac{-1}{2}}{\frac{2}{s}}$$?
mfb said:Sorry typo, this is the formula I meant:
$$\lim_{s \to 0} \frac{\frac{-1}{s}}{\frac{2}{s}}$$
But the more important part was the first question.
That is not the point. It follows the "-infinity/infinity" type. It is easy to simplify it here to see the limit is not infinity, so your original idea cannot work - that was the purpose of the example.Tekneek said:For that formula it would be -1/2.
I don't understand that question.I was thinking it would be infinity because you really can't put down a number with it unless maybe it is 1?
Okay.EDIT: Nvm go it. It ends up being -35/40. Thnx
Tekneek said:Why is the limit not just infinity?
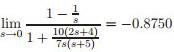
wouldn't it be (1-infinity)/(1+infinity)?
No, check your algebra. The answer in post #1 (-7/8) is correct.Garrulo said:The limit is of (s-1)/(s+(10*(2s+4)/7(s+5) that doing s=0 result in -7/15
The limit as a function approaches 0 is the value that the function approaches as the input (x) gets closer and closer to 0. It is represented by the notation "lim x→0 f(x)" and can be calculated by evaluating the function at values very close to 0.
The concept of limit as it approaches 0 is important in calculus because it allows us to understand the behavior of a function near a specific point. It helps us determine if a function is continuous at a certain point and allows us to find the slope of a curve at that point.
To solve a limit as it approaches 0 algebraically, you need to factor the function and simplify it as much as possible. Then, you can substitute 0 for the variable and evaluate the function. If the result is undefined, you can use other techniques such as L'Hôpital's rule or graphing to find the limit.
Yes, the limit as it approaches 0 can be a different value on the left and right side. This is known as a one-sided limit and it means that the function approaches a different value as the input approaches 0 from the left or the right side. If the left and right limits are different, then the overall limit does not exist.
The concept of limit as it approaches 0 is closely related to the concept of continuity. A function is continuous at a point if the limit as it approaches that point is equal to the value of the function at that point. This means that the function is smooth and has no breaks or sharp turns at that point. Therefore, a function is continuous at a point if and only if the limit as it approaches that point exists and is equal to the function's value at that point.