- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Understanding Why We Need Absolute Value for x
- Thread starter goldfish9776
- Start date
-
- Tags
- Absolute Absolute value Value
In summary: The example in post 11 illustrates ##|\frac{a_{n+1}}{a_n}|>L## for each n, while ##\displaystyle \lim_{n\rightarrow +\infty} |\frac{a_{n+1}}{a_n}| =L##.Maybe a picture will help. When you say ##\lim_{n\to\infty}\left\lvert \frac{a_{n+1}}{a_n} \right\rvert = L##, it means when ##n## is sufficiently large, ##\left\lvert \frac{a_{n+1}}{a_n} \right\rvert
Physics news on Phys.org
- #2
Simon Bridge
Science Advisor
Homework Helper
- 17,876
- 1,660
Look one line up from where you put the circle to see where it comes from.
What happens to the limit when x is a negative number, and you don't have the absolute value?
What happens to the limit when x is a negative number, and you don't have the absolute value?
- #3
goldfish9776
- 310
- 1
Ya, it come from the top. But, why would we need to put iy as absolute value?Simon Bridge said:Look one line up from where you put the circle to see where it comes from.
What happens to the limit when x is a negative number, and you don't have the absolute value?
- #4
Simon Bridge
Science Advisor
Homework Helper
- 17,876
- 1,660
Because if you don't the possibility that x may be negative will give you the wrong limit. Try it and see:
What happens to the limit when x is a negative number, and you don't have the absolute value?
What happens to the limit when x is a negative number, and you don't have the absolute value?
- #5
- 27,222
- 18,632
goldfish9776 said:Homework Statement
why we need to make x as absolute value ? as we can see, the original is x , why we we need to make x as absolute value ? is the working wrong ?
It's using the ratio test. This looks at ##\lim_{k \rightarrow \infty} | \frac{a_{k+1}}{a_k}|##
The modulus should be introduced at the start, not arbitrarily half way through the calculation.
- #6
goldfish9776
- 310
- 1
taking x=-4 , k =2 , the term is -16/27Simon Bridge said:Because if you don't the possibility that x may be negative will give you the wrong limit. Try it and see:
What happens to the limit when x is a negative number, and you don't have the absolute value?
taking x=4 , k=2 the term is 16/27 , i couldn't find out why there is a need to put modulus ?
- #7
- 27,222
- 18,632
goldfish9776 said:taking x=-4 , k =2 , the term is -16/27
taking x=4 , k=2 the term is 16/27 , i couldn't find out why there is a need to put modulus ?
http://tutorial.math.lamar.edu/Classes/CalcII/RatioTest.aspx
- #8
Simon Bridge
Science Advisor
Homework Helper
- 17,876
- 1,660
It's not what happens to the term, it's what happens to the limit.
PeroK has a good link (thanks).
PeroK has a good link (thanks).
- #9
goldfish9776
- 310
- 1
what will happen to the limit ? i really have no idea...Simon Bridge said:It's not what happens to the term, it's what happens to the limit.
PeroK has a good link (thanks).
- #10
goldfish9776
- 310
- 1
well, for this part of the notes, why do we need to make r is between L and 1 , and we take r is larger than L at the lower part ... isn't the L itself is the factor r ?Simon Bridge said:It's not what happens to the term, it's what happens to the limit.
PeroK has a good link (thanks).
Attachments
- #11
Samy_A
Science Advisor
Homework Helper
- 1,242
- 510
No , L doesn't necessarily satisfy ##| \frac{a_{k+1}}{a_k}| \leq L## for k sufficiently large.goldfish9776 said:well, for this part of the notes, why do we need to make r is between L and 1 , and we take r is larger than L at the lower part ... isn't the L itself is the factor r ?
Any r with ##L<r<1## does satisfy ##| \frac{a_{k+1}}{a_k}| \leq r## for k sufficiently large.
As an example, take ##0<L<1##, and define ##(a_n)_n## by:
##a_1=1,\ a_{n+1}=a_n(L+\frac{1}{n})##
Then ##|\frac{a_{n+1}}{a_n}|=L+\frac{1}{n} > L##, but ##\displaystyle \lim_{n\rightarrow +\infty} |\frac{a_{n+1}}{a_n}| =L##.
Last edited:
- #12
Ray Vickson
Science Advisor
Homework Helper
Dearly Missed
- 10,704
- 1,722
goldfish9776 said:well, for this part of the notes, why do we need to make r is between L and 1 , and we take r is larger than L at the lower part ... isn't the L itself is the factor r ?
If ##L = \lim_{n \to \infty} |a_{n+1}/a_n|## then, for any (small) ##\epsilon > 0## we have ##(L-\epsilon) |a_n| < |a_{n+1}| < (L+\epsilon) |a_n|## for all ##n## sufficiently large; essentially, that is the definition of the limit above. We simply cannot conclude that ##|a_{n+1}| \leq L |a_n|##, and in fact, you can construct examples where this is false.
- #13
goldfish9776
- 310
- 1
can you give example for the explanation above ?Ray Vickson said:If ##L = \lim_{n \to \infty} |a_{n+1}/a_n|## then, for any (small) ##\epsilon > 0## we have ##(L-\epsilon) |a_n| < |a_{n+1}| < (L+\epsilon) |a_n|## for all ##n## sufficiently large; essentially, that is the definition of the limit above. We simply cannot conclude that ##|a_{n+1}| \leq L |a_n|##, and in fact, you can construct examples where this is false.
- #14
Samy_A
Science Advisor
Homework Helper
- 1,242
- 510
The example in post 11 illustrates ##|\frac{a_{n+1}}{a_n}|>L## for each n, while ##\displaystyle \lim_{n\rightarrow +\infty} |\frac{a_{n+1}}{a_n}| =L##.goldfish9776 said:can you give example for the explanation above ?
- #15
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,039
- 2,676
Maybe a picture will help. When you say ##\lim_{n\to\infty}\left\lvert \frac{a_{n+1}}{a_n} \right\rvert = L##, it means when ##n## is sufficiently large, ##\left\lvert \frac{a_{n+1}}{a_n} \right\rvert## will be within ##\varepsilon## of ##L##, where we can choose ##\varepsilon>0## arbitrarily. In the picture, that means the terms of the sequence will lie in the green part of the number line. While the terms are close to ##L##, they could be greater than or less than ##L##, so the limit doesn't guarantee that ##\left\lvert \frac{a_{n+1}}{a_n} \right\rvert<L##. However, since ##r>L##, there's some room between ##r## and ##L##, so we can choose ##\varepsilon## such that we can guarantee that ##\left\lvert \frac{a_{n+1}}{a_n} \right\rvert < r## for ##n## sufficiently large.
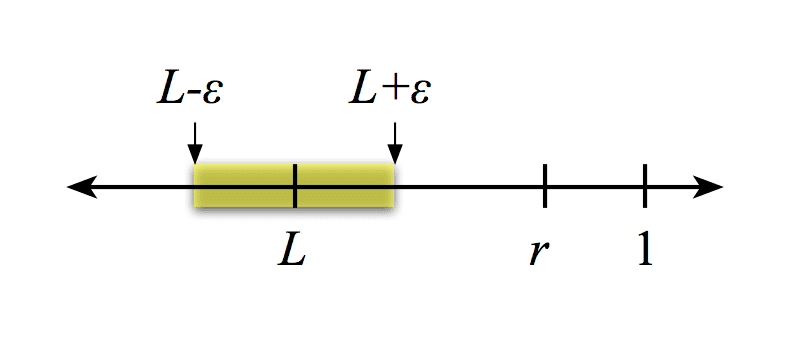
- #16
goldfish9776
- 310
- 1
what is the purpose of not making L =r , but make L less than r ? isn't the L is the factor = r ?vela said:Maybe a picture will help. When you say ##\lim_{n\to\infty}\left\lvert \frac{a_{n+1}}{a_n} \right\rvert = L##, it means when ##n## is sufficiently large, ##\left\lvert \frac{a_{n+1}}{a_n} \right\rvert## will be within ##\varepsilon## of ##L##, where we can choose ##\varepsilon>0## arbitrarily. In the picture, that means the terms of the sequence will lie in the green part of the number line. While the terms are close to ##L##, they could be greater than or less than ##L##, so the limit doesn't guarantee that ##\left\lvert \frac{a_{n+1}}{a_n} \right\rvert<L##. However, since ##r>L##, there's some room between ##r## and ##L##, so we can choose ##\varepsilon## such that we can guarantee that ##\left\lvert \frac{a_{n+1}}{a_n} \right\rvert < r## for ##n## sufficiently large.
View attachment 95310
- #17
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,039
- 2,676
A proof is an argument, so you're essentially asking, why don't you argue it this way instead. So why don't you try finishing the proof with ##r## set equal to ##L##? You'll see it won't work.
What is absolute value and why do we need it for x?
Absolute value is a mathematical concept that represents the distance of a number from 0 on the number line. It is always positive, regardless of the sign of the number. We need it for x because it helps us find the magnitude or size of a number, regardless of its direction.
How do we calculate absolute value for x?
To calculate the absolute value of a number, we remove the negative sign (if there is one) and keep the positive value. For example, the absolute value of -5 is 5, and the absolute value of 5 is also 5.
Why is absolute value important in real-life applications?
Absolute value is important in real-life applications because it helps us measure and compare quantities that have both positive and negative values. It is commonly used in physics, economics, and statistics to represent distances, differences, and deviations.
What is the relationship between absolute value and distance?
The absolute value of a number represents its distance from 0 on the number line. This means that the larger the absolute value, the farther the number is from 0. For example, the absolute value of -10 is greater than the absolute value of -5, so -10 is farther from 0 than -5.
Can absolute value be used for complex numbers or only real numbers?
Absolute value can be used for both real and complex numbers. For real numbers, it represents their distance from 0 on the number line. For complex numbers, it represents their distance from the origin on the complex plane. The absolute value of a complex number is its magnitude or modulus.
Similar threads
-
Calculus and Beyond Homework Help
- Replies
- 3
- Views
- 906
-
Calculus and Beyond Homework Help
- Replies
- 3
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 2
- Views
- 905
-
Calculus and Beyond Homework Help
- Replies
- 8
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 4
- Views
- 283
-
Calculus and Beyond Homework Help
- Replies
- 4
- Views
- 3K
-
Calculus and Beyond Homework Help
- Replies
- 5
- Views
- 326
-
Calculus and Beyond Homework Help
- Replies
- 8
- Views
- 2K
-
Calculus and Beyond Homework Help
- Replies
- 2
- Views
- 820
-
Calculus and Beyond Homework Help
- Replies
- 1
- Views
- 231
Share: