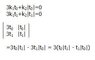- #1
physicsss
- 319
- 0
Given y1=3t, y2=|t|, determine whether the given pair of functions is linearly independent or linearly dependent.
I can't do the Wronskian on this one since y2 is not differentiable at 0, is there any other way to do this?
I can't do the Wronskian on this one since y2 is not differentiable at 0, is there any other way to do this?