- #1
ATY
- 34
- 1
Hey guys,
I need your help. I am not sure if this is the right part of the forum to ask this question.
So I started reading papers about the Lyapunov Exponent, but there is something I do not understand in the formula. Why
 ? It seems logical that we want
? It seems logical that we want
 because we want to get the Exponent at a certain point and therefore the startingpoints should be really close together.
because we want to get the Exponent at a certain point and therefore the startingpoints should be really close together.
I added a text from a book which says, that we have
 , because then my
, because then my
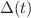 will fluctuate around a finite value, but I have no clue why an exponential function should do this. Maybe somebody can help me.
will fluctuate around a finite value, but I have no clue why an exponential function should do this. Maybe somebody can help me.

I need your help. I am not sure if this is the right part of the forum to ask this question.
So I started reading papers about the Lyapunov Exponent, but there is something I do not understand in the formula. Why
I added a text from a book which says, that we have