Is the Maxwell Ampere Law in Lieberman's Textbook Correctly Stated?

[Decimal]

Hello,

I am currently working through Liebermans textbook on plasma physics. The book starts by simply stating the Maxwell equations, which are used heavily throughout the book. The Maxwell Ampere law however is written in a form that I have never seen before and I am not sure is correct. They state the following, $$ \nabla \times \vec{H} = \vec{J} + \epsilon_0 \frac{\partial \vec{E}}{\partial t}. $$ Here they state that $\vec{J} = \vec{J}_{cond} + \vec{J}_{mag} + \vec{J}_{pol}$. In all versions of this equation that I have come across $\vec{J}_{mag}$ no longer appears, which I thought was the whole point of using $\vec{H}$ instead of $\vec{B}$. What am I missing here? I have included a picture of the explanation in my book.

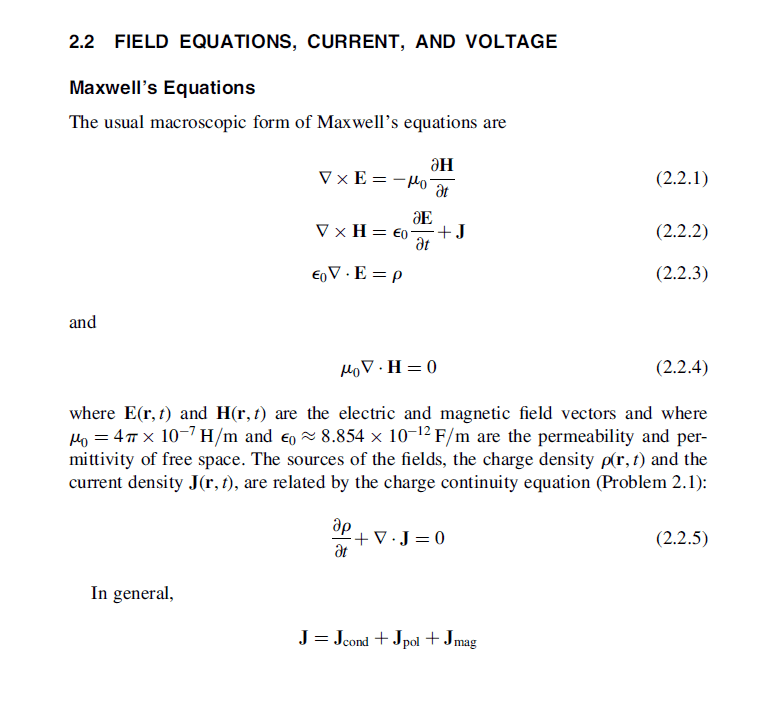
Thanks for the help!

 

[Charles Link]

Looks like they are redefining $H$ as $B=\mu_o H$ instead of $B=\mu H=\mu_o \mu_r H$. $\\$ I can speculate as to why this approach might be taken. The $H$ as it is usually defined, with $B=\mu_o H+M$, rather than being an actual field quantity, can be characterized as a mathematical construction. e.g. the $H$(as it is usually defined) points opposite the magnetization $M$ in a permanent magnet, and is simply the correction to what otherwise would be $B=M$ for geometries other than a cylinder of infinite length (which has no poles, so that $H=0$). $\\$ In defining $B=\mu_o H$, the $H$ is now a true magnetic field that can be measured, (e.g. by a moving test charge), rather than being simply a mathematical construction. (Why the author doesn't simply use $B$ in the equations is a bit of puzzle). $\\$ It can be rather confusing when an author uses the same symbol $H$ for something that is different from what is a common convention throughout most of the other textbooks, but this is my best assessment of what the author is doing. $\\$ Note: The second equation, with the usual definition of $H$ reads (in M.K.S.): $\nabla \times H=J_{conductors}+\frac{\partial{D}}{\partial t}$, which comes from $\nabla \times B=\mu_o J_{total}+\mu_o \epsilon_o \frac{\partial{E}}{\partial{t}}$ with $\mu_o J_m=\nabla \times M$, (with $B=\mu_o H+M$, and $J_{total}=J_{conductors}+J_m +J_p$ with $J_p=\frac{\partial{P}}{\partial{t}}$). Clearly this author redefines $H$ as indicated above.

 

[Decimal]

Thank you so much!

This actually also clears up several other points of confusion I was having with the theory in this book. I did have a suspicion that H was defined differently, but as you said, I was really confused as to why they wouldn't just use $B$ in that case and omit $H$ altogether. Also later in the book where they talk about magnetized plasmas they do explicitly define $B = \mu_0(H+M)$. I suppose their definition of $H$ changes depending on the context.

Thanks again!

 

[Charles Link]

Also later in the book where they talk about magnetized plasmas they do explicitly define B=μ0(H+M)B=μ0(H+M)B = \mu_0(H+M). I suppose their definition of HHH changes depending on the context.

In M.K.S., $B=\mu_o H+M$, or $B=\mu_o(H+M)$. The result is $\mu_o J_m=\nabla \times M$, or $J_m=\nabla \times M$. That part is ok. $\\$ And yes, it is also my assessment that their definition of $H$ depends upon the context. That, IMO, is poor practice. It is likely they know perfectly well that they redefined $H$ to be $B=\mu_o H$, but they should not assume that that is perfectly clear to the reader.

 

[Charles Link]

On a related note, you might find this recent Insights article that I authored to be worthwhile reading: https://www.physicsforums.com/threa...lving-with-the-curl-operator-comments.975978/

 

[Decimal]

On a related note, you might find this recent Insights article that I authored to be worthwhile reading: https://www.physicsforums.com/threa...lving-with-the-curl-operator-comments.975978/

Thanks for the suggestion, I'll take a look! I did find something interesting working through the relevant parts of the book now with the knowledge that $\vec{H}$ is defined differently. In chapter 4 the influence of an external oscillating electric field on an unmagnetized plasma is considered. Here the field is defined is defined as, $$ \vec{E}(t) = Re[\tilde{E} e^{i\omega t}],$$ where $\omega$ defines the oscillation frequency. It is assumed that all quantities in the system oscillate with this frequency. Then using the electron force equation, $$ m_e \frac{d\vec{u}}{dt} = -e\vec{E} - m \nu_m \vec{u}$$ one can derive an expression for the drift velocity $u_x$. Here $\nu_m$ represents the momentum transfer frequency so the second term is an effective friction term with the background gas.

After a bit of algebra one then finds that the total current $\vec{J}_{T} = \vec{J}_{cond} + \epsilon_0 \frac{\partial \vec{E}}{\partial t}$equals, $$ \tilde{J}_{T} = i \omega \epsilon_0 \Big[1-\frac{\omega_{pe}^2}{\omega(\omega-i\nu_m)}\Big]\tilde{E},$$ where $\omega_{pe}$ is the characteristic plasma frequency of the system. I suppose here it's assumed that since in a plasma all charges are free, the only current that exists is the one due to movement of free charges. This all seems ok to me, but then they again go back to using their definition of $\vec{H}$, stating that since $\nabla \times \tilde{H} = \tilde{J}_{T}$, it holds that $$\nabla \times \tilde{H} = i \omega \epsilon_0 \Big[1-\frac{\omega_{pe}^2}{\omega(\omega-i\nu_m)}\Big]\tilde{E} = i \omega \epsilon_p \tilde{E}.$$ Here then they take $\epsilon_p$ as the effective dielectric constant of the plasma, essentially treating the plasma as a dielectric. They state that the equivalent displacement field $\tilde{D}$ is then $\tilde{D} = \epsilon_p \tilde{E}$, which would mean $\nabla \times \tilde{H} = i \omega \tilde{D}$.

So if I understand correctly they do use the "conventional" definiton for $\vec{D}$, being $\vec{D} = \epsilon_0 \vec{E} + \vec{P}$ with $\vec{P}$ the polarization vector. Then from $\nabla \times \vec{H} = \vec{J}_{cond} + \frac{\partial \vec{D}}{\partial t}$ it would appear that they suggest the plasma starts acting as a dielectric with a certain polarization, in absence of any free charges leading to a conduction current.

I think I would interpret this as the free charges inside the plasma essentially acting as bound charges in a dielectric, causing a certain effective polarization. I do still think this whole discussion would be considerably simplified by just using $\vec{B}$ instead of $\vec{H}$, although I assume they really wanted to make this connection to a dielectric.

 

[vanhees71]

I'm just answering to #1. I think the book is heavily flawed. One should look at E&M always through the relativistic view, and there it's clear that the components $(\vec{E},\vec{B})$ and $(\vec{D},\vec{H})$ belong together, and consequently those occur in the homogeneous macroscopic Maxwell equations (which look the same as the microscopic ones) and the inhomogeneous macroscopic Maxwell equations, respectively.

Of course all the beauty of the theory is hidden behind the choice of SI units, but that we can't help, if you want it all written in SI units

$$\vec{\nabla} \times \vec{E}+\partial_t \vec{B}=0, \quad \vec{\nabla} \cdot \vec{B}=0$$
and
$$\vec{\nabla} \times \vec{H}-\partial_t \vec{D}=\vec{j}_{\text{free}}, \quad \vec{\nabla} \cdot \vec{D}=\rho_{\text{free}}.$$
Note that there's a (in some limits arbitrary) split of the charge and the current distributions in "free" and "bound" parts.

You mention the idea of a magnetization current. That's an example for the fact that you can sometimes lump parts of the macroscopic fields to the macroscopic sources and vice versa. In this case the idea is to write
$$\vec{B}=\mu_0(\vec{H}+\vec{M},$$
where $\vec{M}$ is the magnetization density of the medium ($\mu_0$ is simply a conversion constant needed, because in the SI you introduce an extra base units for electric charge, the Coulomb or A s).

Now you can introduce new fields and sources via
$$\vec{B}=\mu_0 \vec{H}' \; \Rightarrow \; \vec{H}'=\frac{1}{\mu_0} \vec{B}= \vec{H}+\vec{M} \, \Rightarrow \; \vec{H}=\vec{H}'-\vec{M}.$$
But then the macroscopic Ampere-Maxwell equation has to be rewritten too:
$$\vec{\nabla} \times (\vec{H}'-\vec{M})-\partial_t \vec{D}=\vec{j}_{\text{free}}$$
or
$$\vec{\nabla} \times \vec{H}'-\partial_t \vec{D}=\vec{j}_{\text{free}} +\vec{\nabla} \times \vec{M},$$
and then you just lump the latter contribution to the current, by writing
$$\vec{j}=\vec{j}_{\text{free}} + \vec{j}_{\text{mag}}, \quad \vec{j}_{\text{mag}}=\vec{\nabla} \times \vec{M}.$$

In addition to these macroscopic Maxwell equations you need also constitutive equations, which relate $(\vec{E},\vec{B})$ with $(\vec{D},\vec{H})$. In linear response approximation that leads to the permittivity and permeability tensors.

Often, particularly in plasma physics, it's also useful to introduce Ohm's Law with the electric conductivity, which in general is also a tensor.

For a thorough discussion about this issue see

A. Sommerfeld, Lectures on Theoretical Physics, vol. 3 (electrodynamics)

In this book it becomes clear, why the various fields belong together in the way described above. Sommerfeld was an early proponent of using SI units in theoretical electromagnetics. If this choice of units were not so inconvenient when doing relativistically covariant electrodynamics, I'd have gotten almost convinced by his arguments ;-))).

For me still the best choice of units is the Heaviside-Lorentz (rationalized Gaussian) units, but that of course doesn't change anything of the foundations discussed above. After all the physics is the same within any system of units.

 

[Decimal]

Thanks for the response vanhees71!

Yeah your explanation pretty much aligns with what I have been taught in previous EM courses, and had the book just used these conventions my problem could have definitely been avoided. I can't really speak to the relativistic side of things yet, but I am taking a relativistic EM course next semester so I'll get there!

Thanks again!