- #1
annamal
- 381
- 33
- Homework Statement
- Previous problem:
(a) A 200-turn circular loop of radius 50.0 cm is vertical, with its axis on an east-west line. A current of 100 A circulates clockwise in the loop when viewed from the east. Earth’s field here is due north, parallel to the ground, with a strength of What are the direction and magnitude of the torque on the loop? (b) Does this device have any practical applications as a motor?
Repeat the previous problem, but with the loop lying flat on the ground with its current circulating counterclockwise (when viewed from above) in a location where Earth’s field is north, but at an angle 45.0° below the horizontal and with a strength of ##6*10^-5## T. See image.
- Relevant Equations
- ##\tau = -IABsin\theta##
I am confused about this, do the black arrows represent the direction of magnetic force?
The torque ##\tau = -IABsin\theta##, where I = current A is area of loop and B is magnetic field strength and I am a little confused how ##\theta## here is 45 degrees when the angle between the normal for the loop and the magnetic field B is 90 degrees unless I am reading the problem incorrectly?
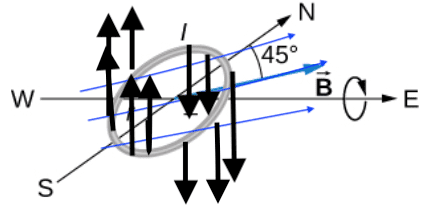
The torque ##\tau = -IABsin\theta##, where I = current A is area of loop and B is magnetic field strength and I am a little confused how ##\theta## here is 45 degrees when the angle between the normal for the loop and the magnetic field B is 90 degrees unless I am reading the problem incorrectly?