Magnitude and direction for the total gravitational force

[Fused]

Please help me with the following problems!

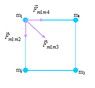
Four 9.5 kg spheres are located at the corners of a squareof side .60m. calculate the magnitude and direction fo the total gravitational force exerted on one sphere by the other three.

*I think I'm supposed to use the forumula : F= G(m1)(m2)/r^2 . where I substitue m1 for the mass of one sphere, and m2 for the mass of the other 2 spheres. I put in .60 for r.
What am I doing wrong, I should be getting 3.2*10^8 but I dont!

Every few hundred years most of the planets line up on the same side of the sun. Calculte the total force on the EArth due to Venus, Juipter and saturn assuming all four planets are in a line. The amsses are Mv=.0815M(of earth), Mj=318Mass(of earth), Ms=95.1M(of earth), and their mean distances from the sun are 108, 150 ,778 and 1430 million km, respectively. What fraction of the sun's force on the Earth is this?

Any hints as to how to even begin to do this one?

 

[TenaliRaman]

Fused,
Before i continue even proposing a solution to either of ur problem.
i would like to tell some things u need to do,
1> draw yourself a diagram of the problem. ...
2> draw the force vectors
3> calculate the necessary angles among the force vectors.

it would be better if u skipped the second problem now and concentrated on the first since that would most prolly help u solve the second ... which is almost identical

Now for the first,
do u know how to resolve forces into horizontal and vertical components?
do u know how to calculate resultant of three forces?
if ur answer to first two questions are yes then that's all u need to know.

-- AI

 

[Fused]

I've done your step 1, I've drawn the vectors, three vectors one going from each of the three spheres to the same one sphere. Am I setting this up correctly? I know how to find the x and y components, but what would the resultant vector look like? I dont' understand how there can be one if all three vectors are pointing to the same object.

 

[TenaliRaman]

sum the horizontal forces , call them say Fx
sum the vertical forces , call them say Fy
magnitude of resultant = sqrt(Fx*Fx+Fy*Fy)
angle of resultant with horizontal = arctan(Fy/Fx)

-- AI

 

[Fused]

I still don't quite understand. This is what I've done so far.

I've drawn four spheres, one at each corner of the square. I've draw vectors from three spheres all pointing to the same one sphere. I've labeled the vectors A (the one pointing in the x direction) vector B, (pointing downwards in the y direction) and point C- the diagonal.
From this I found
Fax = .6
Fbx = 0
Fcx = Fc cosx
Fay=0
Fby=.6
Fcy = Fc sinx

Can I find Fc with the pythagorean theorem. If I do this then the x resultant vectors and the y resultant vectors are the same??

 

[Leong]

$$\begin{multline*} \begin{split} &\vec{F_{ab}}=Force\ exerted\ on\ a\ by\ b\\ &\vec{F_{m_1m_2}}=\frac{Gm_1m_2}{r^2m_1m_2}*(-\vec{j})\\ &\vec{F_{m_1m_3}}=\frac{Gm_1m_3}{r^2m_1m_3}[cos(-45^0)\vec{i}+sin(-45^0)\vec{j}]\\ &\vec{F_{m_1m_4}}=\frac{Gm_1m_4}{r^2m_1m_4}\vec{i}\\ &\vec{F_{m_1}}=\vec{F_{m_1m_2}}+\vec{F_{m_1m_3}}+\vec{F_{m_1m_4}} \end{split} \end{multline*}$$
Do the same with others.

 

[Fused]

What do the j, and i stand for?

 

[Doc Al]

unit vectors

What do the j, and i stand for?

Those are unit vectors. $$\vec{i}$$ points in the +x direction; $$\vec{j}$$ points in the +y direction.

It's one way of showing x and y components of a vector.

 

[Fused]

Those unit vectors are unknowns, right?

 

[Doc Al]

Those unit vectors are unknowns, right?

The unit vectors are just ways to show components of a vector. Here's an example:

Given a force of F that acts at an angle of $\theta$ with respect to the x axis, I can say:
$$F_x = F cos\theta$$
$$F_y = F sin\theta$$

Or I could write it in unit vector notation as:
$$\vec{F} = F cos\theta \vec{i} + F sin\theta \vec{j}$$

Note: Unit vectors are usually written like this $$\hat{j}$$ instead of $$\vec{j}$$

 

[Fused]

So then,could I do this for the first force?

Fm1m2 = (Gm1m2)/r^2 = G(9.5)(9.5)/(.601)^2 = 250.694G ?

 

[Leong]

Fused,
Do you know how to resolve a vector into its x and y components?
Forget about i and j since it confuses you.
Resolve all the forces into x and y components.
the first force you have provided is right, since you gave it a positive value. then downward position is positive, upward position will be negative.
Fm1m2_y=25.0694G N; Fm1m2_x=0 because no component in x direction.
Fm1m4_x=25.0694 N; Sign is choosen here, to left:negative; to right:positive
Fm1m4_y=0 because no component in y direction.
Resolve Fm1m3. you should get a positive value for Fm1m3_y because it points downward and the convention sign has been defined earlier.
You should get a positive value for Fm1m3 _x because it points to right side here.
Add all the x and y components; included the sign as well. finally , you will get a x component and a y component, draw it out, use pytagorean theroem to find its resultant magnitude and angle using trigonometry.