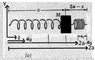
- #1
CGandC
- 326
- 34
1. Homework Statement
The following problem is an example from the book ' Berkely - Waves by Frank S. Crawford Jr '.
Mass 'M' slides on a frictionless surface. It is connected to rigid walls by means of two identical springs, each of which has zero mass, spring constant 'K' and relaxed length 'Ao' .
At equilibrium position , each spring is stretched to length 'A' and thus each spring has tension 'K(A-Ao)' at equilibrium.
Find the total force acting on the mass in the z direction when it is stretched to the right.
note: in the pictures it is written 'a' instead of 'A' , I used 'A' just for convenience
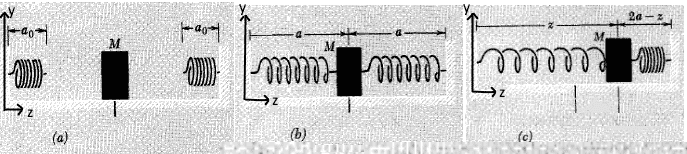
Solution : Fz = -2K(z-A)
Derivation:

2. Homework Equations
Hooke's law : F = -k(x-xo)
3. The Attempt at a Solution
I don't fully understand the derivation to the solution in terms of coordinates, Especially the second term: ' +K(2A-z-Ao) '
Here's my attempt: I redrew the third image as follows:
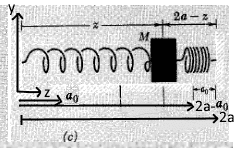
Solving:
Approach 1:
I used Newtons second law on the mass : Fz = -k(z-Ao)+k(z-(2A-Ao) )
Explanation:
'-k(z-Ao)' because of the left spring , the displacement of the mass from the left spring's relaxation point is 'z-A0'
'+k(z-(2A-Ao) )' because of the right spring ( which is compressed) . the displacement is as it is because 'z' is the coordinate of the mass and ' 2A-Ao ' is the relaxation coordinate of the right spring. hence , I wrote ' z - (2A-Ao) '
However,this approach seems false because: Fz=-k(z-Ao)+k(z-(2A-Ao) ) =-kz+kAo+kz-2Ak+kAo=2k(Ao-A)
and this does not match the solution, so after that I tried another approach:
Approach 2:
Fz = -k(z-Ao)-k(z-(2A-Ao) )
Explanation:
everything's the same as in approach 1 , but I only changed sign on the second expression, from
'+k(z-(2A-Ao) )' to '-k(z-(2A-Ao) )'
using this approach I get the right answer:
Fz = -k(z-Ao)-k(z-(2A-Ao) ) = -2k(z-A)
So the questions are:
1.why was my first approach incorrect? ( isn't the sign on the second term suppost to be positive? [ because the right spring moves the mass to the right ] )
2. even though eventually I got to the right answer using approach 2, was this a 'correct' way to solve the problem?
3. was I right to make the displacement corresponding to the first spring as 'z-Ao' and the displacement regarding to the second spring as 'z-(2A-Ao) ' ?
The following problem is an example from the book ' Berkely - Waves by Frank S. Crawford Jr '.
Mass 'M' slides on a frictionless surface. It is connected to rigid walls by means of two identical springs, each of which has zero mass, spring constant 'K' and relaxed length 'Ao' .
At equilibrium position , each spring is stretched to length 'A' and thus each spring has tension 'K(A-Ao)' at equilibrium.
Find the total force acting on the mass in the z direction when it is stretched to the right.
note: in the pictures it is written 'a' instead of 'A' , I used 'A' just for convenience
Solution : Fz = -2K(z-A)
Derivation:
2. Homework Equations
Hooke's law : F = -k(x-xo)
3. The Attempt at a Solution
I don't fully understand the derivation to the solution in terms of coordinates, Especially the second term: ' +K(2A-z-Ao) '
Here's my attempt: I redrew the third image as follows:
Solving:
Approach 1:
I used Newtons second law on the mass : Fz = -k(z-Ao)+k(z-(2A-Ao) )
Explanation:
'-k(z-Ao)' because of the left spring , the displacement of the mass from the left spring's relaxation point is 'z-A0'
'+k(z-(2A-Ao) )' because of the right spring ( which is compressed) . the displacement is as it is because 'z' is the coordinate of the mass and ' 2A-Ao ' is the relaxation coordinate of the right spring. hence , I wrote ' z - (2A-Ao) '
However,this approach seems false because: Fz=-k(z-Ao)+k(z-(2A-Ao) ) =-kz+kAo+kz-2Ak+kAo=2k(Ao-A)
and this does not match the solution, so after that I tried another approach:
Approach 2:
Fz = -k(z-Ao)-k(z-(2A-Ao) )
Explanation:
everything's the same as in approach 1 , but I only changed sign on the second expression, from
'+k(z-(2A-Ao) )' to '-k(z-(2A-Ao) )'
using this approach I get the right answer:
Fz = -k(z-Ao)-k(z-(2A-Ao) ) = -2k(z-A)
So the questions are:
1.why was my first approach incorrect? ( isn't the sign on the second term suppost to be positive? [ because the right spring moves the mass to the right ] )
2. even though eventually I got to the right answer using approach 2, was this a 'correct' way to solve the problem?
3. was I right to make the displacement corresponding to the first spring as 'z-Ao' and the displacement regarding to the second spring as 'z-(2A-Ao) ' ?