- #1
Saitama
- 4,243
- 93
Homework Statement
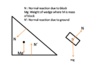
A 45 degree wedge is pushed along a table with constant acceleration A. A block of mass m slides without friction on the wedge. Find its acceleration. (Gravity is directed downwards.)
Homework Equations
The Attempt at a Solution
Let the acceleration of block with respect to wedge be ##b##. Then in the ground frame acceleration of block in x and y direction is
[tex]\ddot{x}=A+b\sin(45^o)[/tex]
[tex]\ddot{y}=-b\cos(45^o)[/tex]
But what do I have to substitute for b here? gsin(45)? Pardon if this is a simple question but I don't have the final answers to this problem so I need someone to check my work.
Thank you.