Masses colliding because of central forces between them

[Satvik Pandey]

Homework Statement

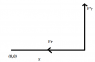
A particle is been acted by a central force exerted by a sphere of mass 'M' at a distance 'x_o' initially from the particle (of same mass). At t=0 the particle has velocity Vt perpendicular to the line joining the particle and the center of the sphere. Find the time at which it collides with the sphere.

It is given that $x_{0}=1m$ and $V_{t}=1m/s$

Homework Equations

$F=\frac { k{ M }^{ 2 } }{ { R }^{ 2 } }$

Also it is given that $4K=1$

The Attempt at a Solution

I first converted the two body problem to a single body problem using reduced mass concept.
Let a reduced mass be placed at distance 'x_o' from point (let it be at origin) exerting Force = $F=\frac { k{ M }^{ 2 } }{ { x }_{ o }^{ 2 } }$
At any general position let the separation between induced mass and the origin be x. Let the radial and tangential velocity at that instant be ${ V }_{ r }$ and ${ V }_{ T }^{ ' }$

From conservation of Angular momentum.
$\mu { x }_{ o }{ V }_{ T }\quad =\quad \mu x{ V }_{ T }^{ ' }$
${ V }_{ T }^{ ' }\quad =\quad \frac { { x }_{ o }{ V }_{ T } }{ x }$......1
Now from Newton's second law.
$\frac { K{ M }^{ 2 } }{ { x }_{ }^{ 2 } } \quad -\quad \frac { \mu ({ V }_{ T }^{ ' })^{ 2 } }{ x } \quad =\quad \mu { a }_{ r }$

$\frac { K{ M }^{ 2 } }{ { \mu x }_{ }^{ 2 } } \quad -\quad \frac { ({ V }_{ T }^{ ' })^{ 2 } }{ x } \quad =\quad { a }_{ r }$

$\frac { K{ M }^{ 2 } }{ { \mu x }_{ }^{ 2 } } \quad -\quad \frac { ({ V }_{ T }^{ })^{ 2 }{ x }_{ o }^{ 2 } }{ { x }^{ 3 } } \quad =\quad -\frac { { V }_{ r }d{ V }_{ r } }{ dx }$

$-\frac { K{ M }^{ 2 } }{ { \mu x }_{ }^{ 2 } } dx\quad +\quad \frac { ({ V }t)^{ 2 }{ x }_{ o }^{ 2 } }{ { x }^{ 3 } } dx\quad =\quad -{ V }_{ r }d{ V }_{ r }$

Integrating
$\frac { K{ M }^{ 2 } }{ { \mu x } } \quad -\quad \frac { { V }t^{ 2 }{ x }_{ o }^{ 2 } }{ { 2x }^{ 2 } } \quad =\quad \frac { { V }_{ r }^{ 2 } }{ 2 } +C$

at, $x\quad =\quad { x }_{ o }$ , ${ V }_{ r }\quad =\quad 0$

so, $C\quad =\quad \frac { K{ M }^{ 2 } }{ \mu { x }_{ o } } -\quad \frac { {V_ { t }}^{ 2 } }{ 2 }$
on putting 'C'

$\frac { 2K{ M }^{ 2 } }{ \mu } (\frac { 1 }{ x } -\frac { 1 }{ { x }_{ o } } )-\quad { V }_{ t }^{ 2 }\quad (\frac { { x }_{ o }^{ 2 } }{ x } -1)\quad =\quad { V }_{ r }^{ 2 }$

As $\mu=M/2$ so

$4K{ M }^{ 2 }\quad (\frac { 1 }{ x } -\frac { 1 }{ { x }_{ o } } )-\quad { V }_{ t }^{ 2 }\quad (\frac { { x }_{ o }^{ 2 } }{ x } -1)\quad =\quad { V }_{ r }^{ 2 }$

$\frac { 1 }{ x } -\frac { 1 }{ { x }_{ o } } -\quad (\frac { { x }_{ o }^{ 2 } }{ { x }^{ 2 } } -1)\quad =\quad { V }_{ r }^{ 2 }$

$\frac { 1 }{ x } -\frac { 1 }{ { x }_{ o } } -\frac { { x }_{ o }^{ 2 } }{ { x }^{ 2 } } +1\quad =\quad { V }_{ r }^{ 2 }$

On substituting the value of $x_{0}$ I got

$\frac { 1 }{ x } -1-\frac { 1 }{ { x }^{ 2 } } +1\quad =\quad { V }_{ r }^{ 2 }$

$\sqrt { \frac { 1 }{ x } -\frac { 1 }{ { x }^{ 2 } } } =\quad \frac { -dx }{ dt }$

$\sqrt { \frac { x-1 }{ { x }^{ 2 } } } =\quad \frac { -dx }{ dt }$

$\int _{ 0 }^{ t }{ -dt\quad =\quad \int _{ { x }_{ 0 } }^{ R }{ \frac { xdx }{ \sqrt { x-1 } } } }$

I don't know if I am right till here or not . It would be nice if anyone could help.

Thank You!

 

[TSny]

Also it is given that $4K=1$

Should this read $4KM = 1$?

Now from Newton's second law.
$\frac { K{ M }^{ 2 } }{ { x }_{ }^{ 2 } } \quad -\quad \frac { \mu ({ V }_{ T }^{ ' })^{ 2 } }{ x } \quad =\quad \mu { a }_{ r }$

It seems to me that the signs are wrong on the left. Also, I'm assuming that the symbol $a_r$ stands for $\ddot{r}$ and not the full radial acceleration in polar coordinates. The $r \dot{\theta}^2$ part of the complete radial acceleration is taken care of in your second term on the left (if the sign is corrected.)

$\frac { K{ M }^{ 2 } }{ { \mu x }_{ }^{ 2 } } \quad -\quad \frac { ({ V }_{ T }^{ ' })^{ 2 } }{ x } \quad =\quad { a }_{ r }$

$\frac { K{ M }^{ 2 } }{ { \mu x }_{ }^{ 2 } } \quad -\quad \frac { ({ V }_{ T }^{ })^{ 2 }{ x }_{ o }^{ 2 } }{ { x }^{ 3 } } \quad =\quad -\frac { { V }_{ r }d{ V }_{ r } }{ dx }$

I don't see how you got the negative sign on the right side in the last equation above.

$-\frac { K{ M }^{ 2 } }{ { \mu x }_{ }^{ 2 } } dx\quad +\quad \frac { ({ V }t)^{ 2 }{ x }_{ o }^{ 2 } }{ { x }^{ 3 } } dx\quad =\quad -{ V }_{ r }d{ V }_{ r }$

You changed the signs on the left, but you didn't change the sign on the right.

Integrating
$\frac { K{ M }^{ 2 } }{ { \mu x } } \quad -\quad \frac { { V }t^{ 2 }{ x }_{ o }^{ 2 } }{ { 2x }^{ 2 } } \quad =\quad \frac { { V }_{ r }^{ 2 } }{ 2 } +C$

You dropped the negative sign on the right that was there in the previous equation.

All of these apparent sign errors seem to cancel so that I agree with what you have at this point!

As $\mu=M/2$ so

$4K{ M }^{ 2 }\quad (\frac { 1 }{ x } -\frac { 1 }{ { x }_{ o } } )-\quad { V }_{ t }^{ 2 }\quad (\frac { { x }_{ o }^{ 2 } }{ x } -1)\quad =\quad { V }_{ r }^{ 2 }$

I don't think the M should be squared on the left. But you made up for that later.

I agree with the rest of your work and your final integral expression for the time looks correct. (I could have overlooked something or made some errors myself.)

EDIT: I now see that some of my disagreements with your signs are due to the fact that you are taking the positive radial direction for $a_r$ to be centripetal rather than centrifugal.

 

[Vaidehi]

Is the sphere fixed (or is it also moving under the influence of the particle)?

 

[ehild]

Homework Statement

A particle is been acted by a central force exerted by a sphere of mass 'M' at a distance 'x_o' initially from the particle (of same mass).
......
$\int _{ 0 }^{ t }{ -dt\quad =\quad \int _{ { x }_{ 0 } }^{ R }{ \frac { xdx }{ \sqrt { x-1 } } } }$

Is R the radius of the sphere? You did not say it in the problem text. And what is K? You also had to state that the central force is an attracting one, so it causes negative radial acceleration.

 

[Vaidehi]

Is the sphere also moving in the problem?

 

[Satvik Pandey]

Should this read $4KM = 1$?It seems to me that the signs are wrong on the left. Also, I'm assuming that the symbol $a_r$ stands for $\ddot{r}$ and not the full radial acceleration in polar coordinates. The $r \dot{\theta}^2$ part of the complete radial acceleration is taken care of in your second term on the left (if the sign is corrected.).

Yes, there $a_{r}$ stands for radial acceleration. .

I don't see how you got negative sign in the right side of you equation
.

There should be -ve sign with $dx/dt$ because $x$ is decreasing with time but acceleration (radial) is $dv_{r}/dt$ and velocity(radial) is increasing with the passage of time there shouldn't be -ve sign. Am I right?

You changed the signs on the left, but you didn't change the sign on the right.

You dropped the negative sign on the right that was there in the previous equation..

Typo. Sorry

 

[Satvik Pandey]

Is R the radius of the sphere?.

$R$ is the radius of the sphere.

You also had to state that the central force is an attracting one, so it causes negative radial acceleration.

If we consider radially inward direction to be positive then:
with passage of time the separation reduced mass and origin decreases. Hence, there should be -ve sign with $dx/dt$ but $\frac { d }{ dt } \left( V_{r} \right)$ should be positive because velocity of approach is increasing with the passage of time. Is right to say so??

 

[Satvik Pandey]

Is the sphere also moving in the problem?

Yes, the sphere is free to move. But we can covert this two body system into a single body system using reduced mass concept in order to solve these kinds of problem easily.

 

[Vaidehi]

Yes, the sphere is free to move. But we can covert this two body system into a single body system using reduced mass concept in order to solve these kinds of problem easily.

Thanks

 

[Vaidehi]

Also, I'm assuming that the symbol $a_r$ stands for $\ddot{r}$ and not the full radial acceleration in polar coordinates. The $r \dot{\theta}^2$ part of the complete radial acceleration is taken care of in your second term on the left (if the sign is corrected.)

In polar coordinates ,taking origin to be at the center of moving sphere ,the force equation is $-\frac{KM^2}{r^2}+r\dot{θ}^2 = \ddot{r}$ . Am I right ? I am fairly new with polar coordinates . What should be the next step ? Should I conserve angular momentum with respect to the Center of Mass ?

 

[TSny]

For this two-body problem, the relative motion of the two objects has been reduced to a one-particle system where the particle moves under the influence of a fixed center of attraction. $r$ denotes the distance of the particle from the center of attraction (origin of the polar coordinates). $r$ also equals the relative separation of the original two bodies.

The central force felt by the particle in the one-particle system has magnitude $KM^2/r^2$ and the mass of the particle is the reduced mass, μ, of the original two bodies.

More on the reduction of a two-body problem to a one-body problem here: http://farside.ph.utexas.edu/teaching/celestial/Celestialhtml/node11.html

In your equation you have left out the mass μ.

Yes, the next step would be to consider how conservation of angular momentum for the single particle allows you to rewrite the $r \dot{\theta}^2$ term as just a function of $r$ alone. Then the differential equation reduces to a second-order differential equation for $r$ as a function of $t$. This should essentially get you Satvik's equation in post #1 where he has $\mu a_r$ on the right side. (However, there are some sign issues due to the fact that I believe Satvik is taking $a_r$ to denote $-\ddot{r}$ rather than $\ddot{r}$).

 

[Vaidehi]

In your equation you have left out the mass μ.

I was not thinking in terms of reduced mass . I was considering the problem as two body problem only . What is the mistake ?

 

[Vaidehi]

For this two-body problem, the relative motion of the two objects has been reduced to a one-particle system where the particle moves under the influence of a fixed center of attraction.

What is the mass at the fixed center of attraction ? Is it equal to the sum of the two bodies involved ?

 

[TSny]

You can see that the three terms in your equation do not have the same dimensions. The first term is a force while the other two terms are accelerations.

If you are going to stay with the two body system, then I don't see how you are setting up the equation. Which of the two bodies are you writing an equation for? I know that you are choosing a coordinate system moving with the center of mass, but I don't know what the symbol r means here. Is it the distance between the two bodies, or the distance from the center of mass to one of the masses?

 

[TSny]

What is the mass at the fixed center of attraction ? Is it equal to the sum of the two bodies involved ?

You don't have to consider any mass at the origin in the reduced one-body problem. The origin is just a fixed point of attraction that attracts the moving body with a force that has the same magnitude as the force between the two bodies in the original problem. You don't need to worry about how the center of attraction creates the force.

 

[Vaidehi]

Thanks .

Do you think reducing to a one body problem is the best way to solve this problem ? Or is there an alternative approach ?

 

[Vaidehi]

You can see that the three terms in your equation do not have the same dimensions. The first term is a force while the other two terms are accelerations.

$-\frac{KM^2}{r^2}+Mr\dot{θ}^2 = M\ddot{r}$?

If you are going to stay with the two body system, then I don't see how you are setting up the equation. Which of the two bodies are you writing an equation for?

The particle , with origin at the center of the sphere .

I know that you are choosing a coordinate system moving with the center of mass, but I don't know what the symbol r means here. Is it the distance between the two bodies, or the distance from the center of mass to one of the masses?

'r' is the distance from the origin(center of sphere) to the particle . Is it wrong ?

 

[TSny]

I do believe the reduction to a one body problem is the best method for this problem (especially if the original two bodies were to have different masses).

For this problem, the two masses are the same. In this case your idea of going to the center of mass is an alternate approach. So, if you go to the center of mass frame it is easy to see that each mass has the same motion (but on opposite sides of the center of mass). If $r$ is the separation distance between the masses, then each mass is a distance $r/2$ from the origin of the CM frame. If you write the equation of motion for one of the masses in the center of mass frame, I believe you get $$-\frac{KM^2}{r^2} = M \left( \frac{\ddot{r}}{2} - \frac{r}{2} \dot{\theta}^2 \right)$$ where $r/2$ is the radial position of the mass and $\theta$ is the angular position. But this can be written as $$-\frac{KM^2}{r^2} = \frac{M}{2} \left( \ddot{r} - r\dot{\theta}^2 \right)$$ which is the equation for a single body of reduced mass $\mu = M/2$ moving under the influence of a fixed central force $-\frac{KM^2}{r^2}$ and the single body is now located at distance $r$ from the origin.

But all of this is pretty much equivalent to doing the formal reduction of the two-body problem to a one-body problem.

 

[TSny]

$-\frac{KM^2}{r^2}+Mr\dot{θ}^2 = M\ddot{r}$?

The particle , with origin at the center of the sphere .

'r' is the distance from the origin(center of sphere) to the particle . Is it wrong ?

If you take the origin at the center of the sphere, then the origin is accelerating (because the sphere accelerates). So, you would be using a non-inertial reference frame. In such a frame you cannot use F = ma without also adding complicated inertial forces.

 

[ehild]

One can start with conservation of energy. What is the energy of the system with the given initial conditions - distance between the masses 1 m, one mass stationary, the other has 1 m/s velocity perpendicular to the line connecting the masses, and 4KM=1?

 

[TSny]

One can start with conservation of energy. What is the energy of the system with the given initial conditions - distance between the masses 1 m, one mass stationary, the other has 1 m/s velocity perpendicular to the line connecting the masses, and 4KM=1?

Good suggestion. Looking at the energy, it appears that the numbers given in the problem lead to no solution. The two objects will continue to separate from one another for all time.

You can also see that there is a problem by looking at Satvik's last equation where the expression $\sqrt{x-1}$ occurs in the integrand. In order for the particle to collide with the sphere, $x$ would need to become less than $x_0 = 1 m$, which makes the square root imaginary.

 

[ehild]

Good suggestion. Looking at the energy, it appears that the numbers given in the problem lead to no solution. The two objects will continue to separate from one another for all time.

.

The energy of the virtual particle with the effective mass M/2 has zero energy, which corresponds to a parabolic orbit in the CoM frame of reference.

By the way, the integral $\int \frac{x dx}{\sqrt{x-1}}$ can be solved (for x>1) with substituting $u=\sqrt{x-1}$

 

[TSny]

The energy of the virtual particle with the effective mass M/2 has zero energy, which corresponds to a parabolic orbit in the CoM frame of reference.

Yes, that's what I get, too.

By the way, the integral $\int \frac{x dx}{\sqrt{x-1}}$ can be solved (for x>1) with substituting $u=\sqrt{x-1}$

Good.

 

[Satvik Pandey]

You can also see that there is a problem by looking at Satvik's last equation where the expression $\sqrt{x-1}$ occurs in the integrand. In order for the particle to collide with the sphere, $x$ would need to become less than $x_0 = 1 m$, which makes the square root imaginary.

Oh! The numbers didn't worked as planned!

I tried to find the the maximum value of velocity with which reduced mass can be projected so that make it's way up to the distance R from the origin.

If it would projected with velocity(tangential) such that force acting on the reduced mass is enough to provide required centripital force then reduced mass will revolve in a circular orbit around the origin.

$\frac { \mu { v }_{ t }^{ 2 } }{ { x }_{ 0 } } =K\frac { { M }^{ 2 } }{ { x }_{ 0 }^{ 2 } }$

${ v }_{ t }=\sqrt { \frac { K{ M }^{ 2 } }{ \mu { x }_{ 0 } } }$

So for ${ v }_{ t }<\sqrt { \frac { 2K{ M }^{ } }{ { x }_{ 0 } } }$ the particle surely collides with the sphere. Right??

 

[ehild]

If it would projected with velocity(tangential) such that force acting on the reduced mass is enough to provide required centripital force then reduced mass will revolve in a circular orbit around the origin.

$\frac { \mu { v }_{ t }^{ 2 } }{ { x }_{ 0 } } =K\frac { { M }^{ 2 } }{ { x }_{ 0 }^{ 2 } }$

${ v }_{ t }=\sqrt { \frac { K{ M }^{ 2 } }{ \mu { x }_{ 0 } } }$

So for ${ v }_{ t }<\sqrt { \frac { 2K{ M }^{ } }{ { x }_{ 0 } } }$ the particle surely collides with the sphere. Right??

It depends on the radius of the sphere. The particle moves along an ellipse if the energy is negative, and the shape of the ellipse is not influenced by the size of the sphere.