- #1
alice22
- 35
- 0
Use English to explain what this is showing.
Also prove it!
alice22 said: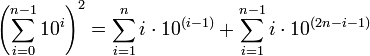
Use English to explain what this is showing.
Also prove it!
alice22 said: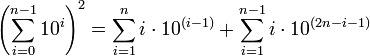
Use English to explain what this is showing.
Also prove it!
HallsofIvy said:The simplest thing to do is to look at what it says for some small n- say n= 3.
[tex]\left(\sum_{i=0}^{3-1}10^i\right)^2= \left(10^0+ 10^1+ 10^2\right)^2= (1+ 10+ 100)^2= 111^2[/tex].
[tex]\sum_{i=1}^n i10^{i-1}= 1(10^0)+ 2(10^1)+ 3(10^2)= 321[/tex]
[tex]\sum_{i=1}^{n-1} i10^{2n-i-1}= 1(10^4}+ 2(10^3)= 1200[/tex]
It's easy to calculate that [itex]111^2= 12321= 1200+ 321[/itex].
[itex]11^2= 121[/itex], [itex]111^3= 12321[/itex], [itex]1111^2= 1234321[/itex] , etc.
Do you see the pattern?
[tex]\sum_{i=1}^{n-1} i10^{2n-i-1}[/tex]
is the first part- the 1234... Do you see how it is counting "down" because of the [itex]10^{2n-i-1}[/itex]?
[tex]\sum_{i=1}^n i10^{i-1}[/tex]
is the last part: 321
To prove the solution to a math problem, you need to show that the answer you have obtained is correct and can be supported by evidence and logical reasoning. This can be achieved through various methods such as mathematical induction, direct proof, or proof by contradiction.
Proving the solution to a math problem is important because it helps to validate the answer and ensure that it is reliable and accurate. It also allows others to understand and replicate the solution, leading to a better understanding of the problem.
Yes, there are various methods that can be used to prove the solution to a math problem. The choice of method depends on the type of problem and personal preference. Some common methods include mathematical induction, direct proof, proof by contradiction, and proof by contrapositive.
Some common mistakes to avoid when proving the solution to a math problem include incorrect application of the chosen method, skipping steps in the proof, and making assumptions without sufficient evidence. It is important to carefully follow each step and clearly explain each step in the proof.
To improve your skills in proving the solution to math problems, it is important to practice regularly and seek help from experienced mathematicians or teachers. Additionally, familiarizing yourself with different proof techniques and understanding the underlying concepts of mathematical reasoning can also help improve your skills in proving solutions.