MatLab / Vector Field Physics

[PropulsionMan]

So, this is going to be pretty hard for me to explain, or try to detail out since I only think I know what I'm asking, but I could be asking it with bad wording, so please bear with me and ask questions if need-be.

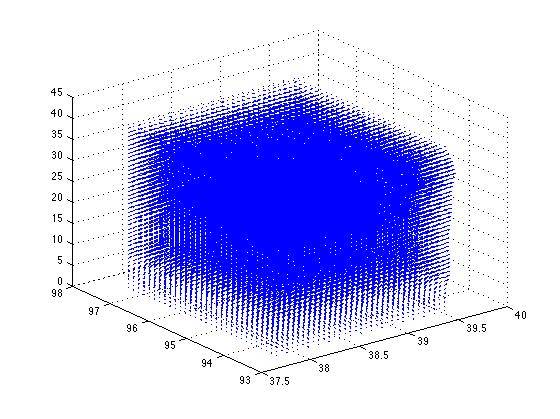
Currently I have a 3D vector field that's being plotted which corresponds to 40 levels of wind vectors in a 3D space (obviously). These are plotted in 3D levels and then stacked on top of each other using a dummy altitude for now (we're debating how to go about pressure altitude conversion most accurately--not to worry here). The goal is to start at a point within the vector space, modeling that point as a particle that can experience physics, and iteratively go through the vector field reacting to the forces, thus creating a trajectory of sorts through the vector field.

Currently what I'm trying to do is whip up code that would allow me to to start a point within this field and calculate the forces that the particle would feel at that point and then establish a resultant force vector that would indicate the next path of movement throughout the vector space.

Right now I'm stuck in the theoretical aspects of the code, as I'm trying to think through how the particle would feel vectors at a distance.

Any suggestions on ways to attack this problem within MatLab or relevant equations to use?

 

[pasmith]

I would solve a 6-dimensional system of ODEs for the position $\vec x(t)$ of the particle (which accounts for three of the dimensions) and its velocity $\vec v(t)$ (which accounts for the other three dimensions). By definition we have
$$\frac{d \vec x}{dt} = \vec v$$
and the equation of motion is then
$$m\frac{d \vec v}{dt} = -k(\vec x)\left\|\vec v - \vec u(\vec x)\right\|\left(\vec v - \vec u(\vec x)\right) + m \vec g$$
where $m$ is the particle's mass, $k > 0$ a coefficient which will depend on the size and shape of the particle and conceivably also on air pressure and thus altitude, $\vec u$ the wind velocity and $\vec g = g(0,0,-1)$ is the gravitational acceleration.

The idea is that air resistance should be proportional to the square of the velocity of the particle relative to the air, and in the direction opposite to the relative velocity.

MATLAB should be fully capable of solving this system numerically given the initial position and velocity of the particle. You may end up having to interpolate to find the wind velocity at $\vec x$ from your data.