- #1
synkk
- 216
- 0
For part b:
Could anyone why it is + or - 3? I really don't understand why there would be two solutions as det|P| as it would just be the absolute value of P, meaning just +ve?
It's "±" because your equation has the absolute value of the determinant of p .synkk said: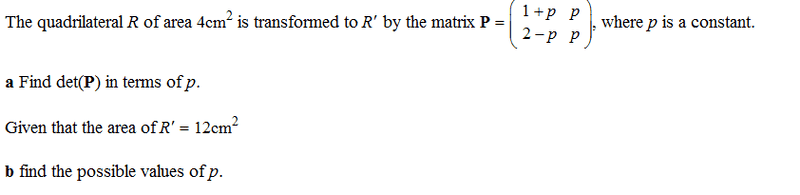
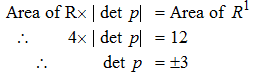
For part b:
Could anyone why it is + or - 3? I really don't understand why there would be two solutions as det|P| as it would just be the absolute value of P, meaning just +ve?
You seem to be confusing P (the matrix) and p (a number). Uppercase and lowercase are significant here, and you seem to be ignoring the difference.synkk said: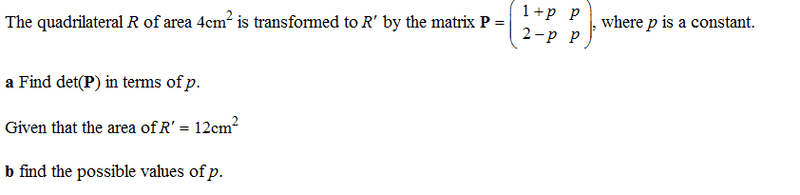
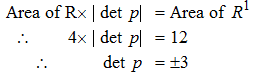
For part b:
Could anyone why it is + or - 3? I really don't understand why there would be two solutions as det|P| as it would just be the absolute value of P, meaning just +ve?
SammyS said:It's "±" because your equation has the absolute value of the determinant of p .
Mark44 said:You seem to be confusing P (the matrix) and p (a number). Uppercase and lowercase are significant here, and you seem to be ignoring the difference.
The notation |P| doesn't mean "absolute value" of P; it is the determinant of P, also written as det(P).
What you show as |det p| makes no sense, because you're not taking the deteriminant of the number p - you want the determinant of the matrix P.
OK, then that's an error in the book. Apparently the author got confused between P and p.synkk said:What is shown in the OP is what the book has shown, not me.
synkk said:Thanks for your input so far.
SammyS said:It's "±" because your equation has the absolute value of the determinant of p .
synkk said:Why?
SammyS said:The solution to
4|x|=12
is
x = ±3 .
Do you agree?
synkk said:No I've never learned this before, could you explain it please?
d2j2003 said:the solution to 4|x|=12 is x=±3 BECAUSE if you plug x back in it works for both 3 and -3 ie. if you only list one of these as a solution then you have not completely solved the equation.
Therefore if you have 4|det P|=12 then |det P| = 3 meaning that det P can be either 3 or -3
make sense?
A matrix is a collection of numbers arranged in a rectangular or square grid. It is used in mathematics to represent and solve systems of linear equations, transform geometric shapes, and perform calculations in various areas of science and engineering.
The determinant of a matrix is a value that can be calculated from the elements of the matrix and represents the scaling factor of the linear transformation described by the matrix. It is important because it is used to determine if a matrix is invertible, and it also has applications in solving systems of linear equations and finding eigenvalues.
The determinant of a matrix can be found by using the formula det|A| = a11b22 - a12b21, where a11 and b22 are the elements of the main diagonal and a12 and b21 are the elements of the other diagonal. This formula can be extended to larger matrices by using the Laplace expansion method.
The determinant of a matrix can be used to determine the number of solutions for a system of linear equations represented by the matrix. If the determinant is non-zero, then the system has a unique solution. If the determinant is equal to zero, then the system has either no solutions or infinitely many solutions.
Yes, the determinant of a matrix can be negative. The sign of the determinant depends on the order of the rows and columns in the matrix. If the number of row exchanges needed to bring the matrix to upper triangular form is odd, then the determinant will be negative. Otherwise, it will be positive.