- #1
ericdavid
- 9
- 0
Hi to everyone,
I'm optimizing a nonlinear function but I'm struggling to achieve it. The function is the following:
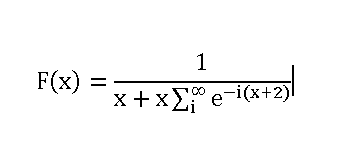
X and i are relationed so i doesn't go to infinite. Do you have any idea how to maximize this function?
Thanks in advance,
Eric
I'm optimizing a nonlinear function but I'm struggling to achieve it. The function is the following:
X and i are relationed so i doesn't go to infinite. Do you have any idea how to maximize this function?
Thanks in advance,
Eric