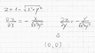- #1
asi123
- 258
- 0
Homework Statement
Hey.
I need to find maximum and minimum for this function, as you can see, I found (0,0) as a "suspicious point" (I don't know how it's called in English ).
My question is, how can I determine if it's Max or Min (if it's possible)?
I know the test of the second derivative, but how should I get it? I mean should I use the definition of the derivative? because I think there is a problem around the point (0,0).
Any idea guys?