- #1
AirForceOne
- 49
- 0
A particle is initially at, and its time history after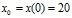 is given by:
is given by: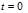
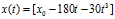
If this equation is differentiated and solved for time when v=0, one answer will be negative and one will be positive. What does the negative answer mean?
So my initial thought was that there's no such thing as negative time. Obviously, however, that's not the correct answer, because let's face it; the question can't be that easy.
The question could have started with just the velocity equation and asked us to find the meaning behind the negative time when we set v=0. However, the question did not start with just the velocity equation, leading me to believe that the answer is related to the position equation in some way.
So I'm thinking...position...negative time...well if I plug in t= -sqrt(2) into the position equation, I get -150 meters. I'm lost. I give up. Help?
Thanks.
PS- This question is from a college level dynamics course...the concepts in this chapter involve differential equations...if that helps at all.
Last edited: