- #1
shaltera
- 90
- 0
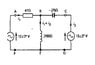
Homework Statement
Use mesh current analysis to determine I1
Homework Equations
Loop 1
47i1+j100(i1+i2)-12=0
(47+j100)i1+j100i2=12
Loop 2
-j75i2+j100(i1+i2)-10=0
j100i1+j25i2=10
The Attempt at a Solution
Homework Statement
Homework Equations
j100i1+j25i2=10 (-4)
-j400i1-j100i2=-40
(47+j100)i1+j100i2=12
-j400i1+(47+j100)i1=-38
j400i1-i1(47+j100)=38
(-47-j300)i1=38
Is it correct?
Attachments
Last edited by a moderator: