- #1
StarMan1234
- 7
- 0
Homework Statement
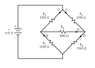
In the figure ε = 9.55 V, R1 = 2090 Ω, R2 = 3360 Ω, and R3 = 4440 Ω. What are the potential differences (in V) (a) VA - VB, (b) VB - VC, (c) VC - VD, and (d) VA - VC?
https://www.google.com/search?q=mes...rcuits.com%2Fvol_1%2Fchpt_10%2F3.html;430;283
This figure is NOT the same as my problem, although the wires are the same. The resistors are in a different order. R2 is on the TOP LEFT and BOTTOM RIGHT, R3 is in the MIDDLE, and R1 is on the TOP RIGHT and BOTTOM LEFT. Hope this makes sense. R4 and R5 are only in the image I provided.
In the problem I define currents (I1 throught I5) as corresponding to the resistors in the diagram.
Homework Equations
Junction Rule
Kirchhoff's Rule
The Attempt at a Solution
I2=I3+I5
I4=I1+I3
Loop Equations:
E-I1R2-I4R1=0
E-I2R1-I3R3-I4R1=0
E-I1R2-I3R3-I5R2=0
E-I2R1-I5R2=0
Anyone familiar with this type of problem?