- #1
g48dd
- 4
- 1
- TL;DR Summary
- Determine the time period it takes for three different cycles to intersect at the same time.
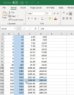
I wanted to look at Milankovitch cycles and each cycle like a clock and that would mean we have 3 clocks each one moving at a different speed. We have a 100,000 year clock (Eccentricity), a 41,000 year clock (Obliquity), a 26,000 year clock (Procession). I want to start all the clocks at the same time. I am looking for a cycle of when all three clocks are once again at their starting point at the exact same time. I don’t know if there is a name for that cycle. I didn't think this would be that difficult to figure out; I’m not great with math but OK with a spreadsheet given some time. I thought that sense Eccentricity is the longest cycle why not just find where Obliquity and Procession divide into 100,000 years evenly at the same time. I am assuming this would mark the end of one full Milankovitch cycle and the beginning of the next. I used a spreadsheet for this because I have no idea how to write an equation for it. Excel will only work with so many digits, so I had to reduce 100,000 to 10, 41,000 to 4.1, and 26000 to 2.6 and then when I get my final number, I multiply by 10^4. That said the earliest occurrence of both Obliquity and Procession dividing in evenly at the same time was when Eccentricity was on its 5,330th completed cycle. So 5330 x 10^4 would be 53,300,000 years. I have uploaded a screen shot of my Excel spreadsheet and I have collapsed hundreds of rows. Column A 1-1,000,000, Column B 10*A1 carried down, Column C is the result in B1/4.1 and Column D is the result in B1/2.6 and I rounded to 4 decimals. At line 533 they all lined up. I then multiplied 5330 by 10^4 and got 53,300,000 years. So my questions are; would this represent a full Milankovitch cycle? Is there a name for that? Am I even thinking about this correctly and if not, could you suggest some reading or a video. Thank You