- #1
julianwitkowski
- 133
- 0
Hey thanks for reading:)
I'm trying to learn calc and I thought it would help if I could figure out how to do this...
For school I have a physics paper on artificial gravity and how it could work... I didn't post this in HW help because It's more of a written thing and I just got sidetracked by boredom.
Basically my idea is to find the min rpm and min radius for an artificial gravity via centripetal force wheel based on the percentage of Earth gravity you want within said height of the floor.
r = radius
μ = rpm
g = 9.81
n = distance from floor to keep % within
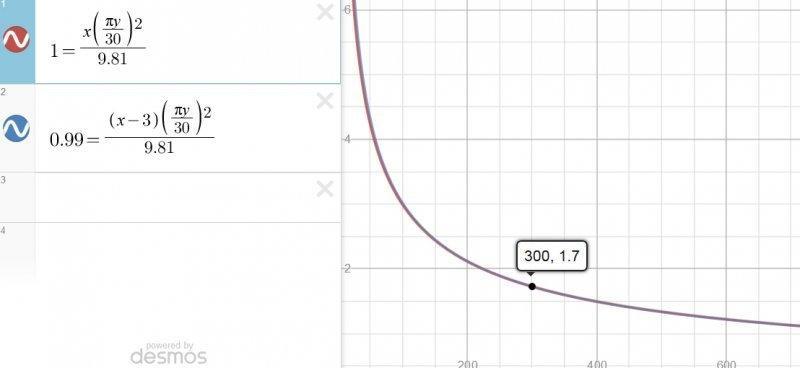
1 = r (π⋅μ /30)2 / g
0.99 = (r-n)(π⋅μ /30)2 / g
I set some parameters in this graph to keep local g within 3meters of the floor be within 99% of Earth.
My algebra and calc still aren't good enough to do this although I am dying to find out.
I can do this easily with derivative problems using only one variable but I don't want to be cheap and set a proportion for radius to rpm, Without doing that I suspect this might have to be solved with partial derivatives but I don't really know.
I solved it with a graph first, here is what it looks like... Just two lines intersecting,
Is there some general format to solve where two lives intersect?
x = radius
y = rpm
 I'm not sure what my next step should be here..
I'm not sure what my next step should be here..
I think I need a decent hint to get going..
I don't know if this is going the right direction although wolfram was able to solve it so maybe its on the right track at least... p = percentage difference from 100% g.
1 - [r (π⋅μ /30)2 / g] + [(r-n)(π⋅μ /30)2 / g + p] = 1
If you read this far, thank you.
:)
I'm trying to learn calc and I thought it would help if I could figure out how to do this...
For school I have a physics paper on artificial gravity and how it could work... I didn't post this in HW help because It's more of a written thing and I just got sidetracked by boredom.
Basically my idea is to find the min rpm and min radius for an artificial gravity via centripetal force wheel based on the percentage of Earth gravity you want within said height of the floor.
r = radius
μ = rpm
g = 9.81
n = distance from floor to keep % within
1 = r (π⋅μ /30)2 / g
0.99 = (r-n)(π⋅μ /30)2 / g
I set some parameters in this graph to keep local g within 3meters of the floor be within 99% of Earth.
My algebra and calc still aren't good enough to do this although I am dying to find out.
I can do this easily with derivative problems using only one variable but I don't want to be cheap and set a proportion for radius to rpm, Without doing that I suspect this might have to be solved with partial derivatives but I don't really know.
I solved it with a graph first, here is what it looks like... Just two lines intersecting,
Is there some general format to solve where two lives intersect?
x = radius
y = rpm
I think I need a decent hint to get going..
I don't know if this is going the right direction although wolfram was able to solve it so maybe its on the right track at least... p = percentage difference from 100% g.
1 - [r (π⋅μ /30)2 / g] + [(r-n)(π⋅μ /30)2 / g + p] = 1
If you read this far, thank you.
:)