- #1
integra2k20
- 35
- 0
Model Airplane Question - centripetal acceleration and summing forces
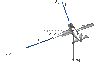
A model airplane of mass 0.760 kg flies in a horizontal circle at the end of a 58.0 m control wire, with a speed of 35.0 m/s. Compute the tension in the wire if it makes a constant angle of 20.0° with the horizontal. The forces exerted on the airplane are the pull of the control wire, the gravitational force, and aerodynamic lift, which acts at 20.0° inward from the vertical as shown in Figure P6.71.
OK, I've been working on this one for 20 minutes and i have no idea. last question left on my problem set.
I found the centripetal acceleration by finding the radius of the circle in which the plane flies--since it flies on an angle on the string, i found this to be 54.40 m (NOT the 58m from the question--is this right?) my centripetal Acceleration was 22.47m/s^2
Next i summed the forces, got
SUM(Fr)=> Ac = Fsin(theta)+Tcos(theta)
SUM(Fy)=> Tsin(theta)+W=Fcos(theta)
from here i solved the 2nd equation for "F" and pluged it into the first, solved for t. I got 18.56, which is wrong. Any ideas? I am sure i missed some thing small, thanks for the help!
A model airplane of mass 0.760 kg flies in a horizontal circle at the end of a 58.0 m control wire, with a speed of 35.0 m/s. Compute the tension in the wire if it makes a constant angle of 20.0° with the horizontal. The forces exerted on the airplane are the pull of the control wire, the gravitational force, and aerodynamic lift, which acts at 20.0° inward from the vertical as shown in Figure P6.71.
OK, I've been working on this one for 20 minutes and i have no idea. last question left on my problem set.
I found the centripetal acceleration by finding the radius of the circle in which the plane flies--since it flies on an angle on the string, i found this to be 54.40 m (NOT the 58m from the question--is this right?) my centripetal Acceleration was 22.47m/s^2
Next i summed the forces, got
SUM(Fr)=> Ac = Fsin(theta)+Tcos(theta)
SUM(Fy)=> Tsin(theta)+W=Fcos(theta)
from here i solved the 2nd equation for "F" and pluged it into the first, solved for t. I got 18.56, which is wrong. Any ideas? I am sure i missed some thing small, thanks for the help!
Attachments
Last edited: