Modulus of rupture at an angle

[patehi]

Homework Statement

Hi guys, i came across a paper about an Investigation of pencil-lead breaks as acoustic Emission sources by Markus G.R. Sause (it's downloadable everywhere).

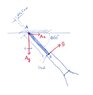
The Setup of the Experiment can be seen in the Picture i attached. Now the Problem i have is to find the correct formula on how to find the breaking force of lead, where the elastic modulus and density are defined.
E=10.5 Gpa, ρ=1.78 Mg/m3.
In the table below, the calculated forces are listed in the table "Force (experimental)".

My attempt is to use the formula of Modulus of rupture, E = M.y/I and get the value for Bending Moment. For the sake of example, i am using 0.5 mm Diameter, 60° angle, 4 mm lead length.

Assuming that i am using the correct formula, i calculated the Bending Moment on the System.
This is where i stuck since I am not sure what are all Forces acted on the lead. (Please see my attempt in the attachment).

Homework Equations

Once all Forces are known, use force Equilibrium where Fx=0, Fy=0, M=0.

The Attempt at a Solution

Please see the Images i attached.

Thanks! I appreciate your help!

 

[CivilSigma]

If your assuming that the lead can move in and out freely, then I agree with your sketched forces. (you model the tip of the pencil as a roller, and end as a pin).

 

[patehi]

hi thanks for the reply!

I forgot to mention that the lead is fixed, and can't move in and out freely.

 

[Nidum]

There are problems with both your experimental method and your theoretical calculations .

(1) Depending on the setting angle there may be :

(a) Significant axial load on the lead .
(b) Slippage of the lead along the load cell surface sufficient to change the problem geometry .

(2) The lead is only poorly supported in bending by the quill tube in the pen . You can't assume a fully rigid fixing .

(3) There is a stress concentration in the lead at the point where it contacts the quill tube during bending .

(4) The actual mechanics of breakage for the lead are not going to be easy to determine . Certainly a more detailed calculation for breaking load will be needed than you have so far attempted .

 

[Nidum]

Would you like to make an attempt at analysing the 0, 5 mm dia x 4 mm long lead + 60° setting angle case in detail ?

Show us what you come up with and then we can discuss any difficulties and see how to make your experimental and theoretical results agree better .

 

[patehi]

i have revised the forces acting on the System.
As you can see, S is the stress concentration at the quill and P is longitudinal stress of lead. F is the force pushing the whole System onto the load cell.
In the paper it is however not defined at which length was the mechanical pencil clamped, so i define it as "l".

This is what i came up with.

upload pic

Am i going in the right direction?

 

[Nidum]

Sorry - I have only just noticed your reply post .

Yes - at first glance that looks like a much more realistic model . Have you got some numerical results for breakage loads yet ?

 

[patehi]

i will try to get the numerical results, but just for reassurance, the force which registers on the load cell would be the Ay, correct? If that's the case, i should calculate Ay?

 

[CivilSigma]

The force F is given and it is the applied force to write.

What you will be doing is correlating the yield moment to applied force F.

So, you will need to calculate the bending moment diagram.

So, first thing to do is to analyse the lead segment. You will need to calculate Ay, Ax, S and P. Note that the forces Ay and Ax each have two other forces - both parallel and perpendicular to the lead. We can neglect the parallel forces to the lead since they do not contribute to the bending moment diagram.

After bending moment diagram analysis, you will obtain the maximum moment the lead undergoes at the assumed breaking applied force 'F' and you can compare your results to the experimental ones.