What Are Some Tips for Starting Moment Couple Problems?

[caddyguy109]

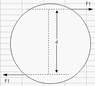
Okay, having some problems figuring out how to start this problem on a moment couple:
http://img347.imageshack.us/img347/6939/problem55hb.jpg

And the same thing for this one:
http://img347.imageshack.us/img347/2488/problem64sx.jpg

Any tips on how to start each one? I think I just need a jumpstart...

 

[hotvette]

Fundamental methodology for statics:

1. Draw free body diagrams of objects w/ forces and moments

2. $\Sigma F_i = 0$

3. $\Sigma M_i = 0$

 

[caddyguy109]

Okay, that makes sense, and I just finished the first 4 of my 6 problems correctly, BUT I'm still a little stuck on just starting the last 2.

For the first one there, what exactly should I first do? I understand the situation, and what's happening, just trying to get what needs to be calculated.

Can you be a little more descriptive?

 

[hotvette]

The last 2 meaning the ones you posted links for? We'll, I'm not sure what part you are stuck on:

1. Drawing the free body diagrams for each object? I guess the only thing I can think of to add is a hint that touching objects have equal and opposite forces on each other when you split them apart into free body diagrams

2. Sum of forces = 0? The only hint I can think of is to sum the forces separately in each coordinate direction. Treat each object separately.

3. Sum of moments = 0? To clarify, moment about the center of mass. If a circular object of radius r has a tangengial force f, the moment about the center of mass is rf. Make sure to keep the directions straight (i.e. CW vs CCW). Treat each object separately.

The equations you get from 2 & 3 will generally be n equations in n unknowns that you can solve.

Hope this helps.

 

[caddyguy109]

Okay, well, it's still not clicking.

1) To find the force N, how should I be setting up the moments? I completely understand how the moment couple is equal and opp., but do I start by using the radius of one of the rollers and the given tension force as the moment?

Like this?: Ma=(r)(Fsin(theta))=(0.025m)(75N)sin(90)=0.375Nm

Is that a step I would take for the first posted problem?

 

[caddyguy109]

----------

 

[caddyguy109]

Again...

#1) Should I find a moment on one of the rollers using the tension force and radius? If so, then what?

#2) If I find the moments acting on each handle, then how to combine them and get the direction/space angles of the resultant?

I have lots of examples, but none like either of these problems.

 

[caddyguy109]

Can anyone just give me a first line for the first equation/step in the first one?

I get the "theory" points, but am confused because of the system in the problem.

 

[hotvette]

This is strange. I posted a reply last night but don't see it. I don't think I was dreaming...

Anyway, I'm not sure this is valid, but I think it is.

1. Consider the two rollers as a single object. At the top of the object is a normal force and a tangential one. Same with the bottom.

2. Summing forces in both coordinate directions should be easy.

3. Summing the moments can be a bit tricky. The moment to be summed is about the center-of-mass. Think about where the center of mass is of the combined rollers.

Hope this helps get you in the right direction.

 

[caddyguy109]

This is strange. I posted a reply last night but don't see it. I don't think I was dreaming...

Anyway, I'm not sure this is valid, but I think it is.

1. Consider the two rollers as a single object. At the top of the object is a normal force and a tangential one. Same with the bottom.

2. Summing forces in both coordinate directions should be easy.

3. Summing the moments can be a bit tricky. The moment to be summed is about the center-of-mass. Think about where the center of mass is of the combined rollers.

Hope this helps get you in the right direction.

Okay. So "Summing forces in both coordinate directions" means adding the x (T) and y (N) forces at both the top and bottom to get the total force acting on each roller? Like T+N=F in the equation M=rFsin(theta)?

And the center of the mass should be right where the two tangentially touch one another?

 

[caddyguy109]

Like this?
http://img392.imageshack.us/img392/8307/problem5start5sm.jpg

Oh no, wait...would I keep the r as just r, and then plug that in when finding the total moment of the system--the center point of the system?

 

[caddyguy109]

Okay, went over it again:
M=(r)(F)

At top:
(F)=(-Ti-Nj)
so MA=(-r)(Ti+Nj)

At bottom:
(F)=(Ti+Nj)
so MB=(r)(Ti+Nj)

Looking right so far? Then, to add them together, I have to use r= the center point of the whole system? What about the angle?

 

[caddyguy109]

How about this:
M=(r)(F)

At top:
(F)=(-Ti-Nj)
so MA=(-r)(Ti+Nj)

At bottom:
(F)=(Ti+Nj)
so MB=(r)(Ti+Nj)

Then:
Meq=MA+MB=[(r)(Ti+Nj)]+[(r)(Ti+Nj)]
Meq=(-r)[(Ti+Nj)]
=(-rTi)+(-rNj)
-rNj=Meq+rTi (Meq goes to zero?)
Nj=(rTi)/(-r)
Nj=(-Ti)
Nj=(-15N) Something's wrong, this can't be right, but where did I flub up? I think the radius to the center moment needs to be included, but couldn't see how, since it canceled out, or so I thought...

Input please?!

 

[caddyguy109]

Where'd I "miss"?

 

[caddyguy109]

Please, anybody, I really have to get these done!

Anyone know or are they just weird problems?

 

[hotvette]

I hope we're talking about the first problem, the one with the 2 rollers between the belts.

Re summing the forces, actually that's already done for you in the problem, and the appropriate coordinate system for that is horizontal (x) and vertical (y) because those are the directions the forces lie in. All this means is that the N at the top is the same as N in the bottom but in the opposite direction. So, $\Sigma F_y = 0$ just means N - N = 0, or N = N, which is already given. It might make more sense if the top one had been labeled N1 and bottom one N2. Anyway, they have to be equal to each other because there are no other forces in the y direction.

Now, take the x direction. $\Sigma F_x = 0$ just means that T - T = 0. Again, trivial in this problem. So, forget about summing forces because it's already done.

Now, for the moments. By the way, you are correct that the center of mass is where the 2 rollers touch. There are 4 moments acting at the center of mass. At the top you have N times it's 'lever arm' (don't know what terminology you use), T times its lever arm acting in the opposite direction as the first one. You also have the same situation at the bottom. Thus, all you have to do is calculate the lever arms based on the geometry, multiply those by the forces (keeping the CCW and CW directions correct), sum them, set the sum equal to zero, and solve for N (because T is expressed in terms of N). You have single equation in N.

If you aren't sure what I mean by 'lever arm', a moment is determined by multiplying a force by a distance that is perpendicular to the direction of the force and through the center of mass. In other words, the force and the lever arm are at right angles.

P.S. I hope your other post about nobody responding was referring to the 2nd problem, not this one.

 

[caddyguy109]

I hope we're talking about the first problem, the one with the 2 rollers between the belts.

Re summing the forces, actually that's already done for you in the problem, and the appropriate coordinate system for that is horizontal (x) and vertical (y) because those are the directions the forces lie in. All this means is that the N at the top is the same as N in the bottom but in the opposite direction. So, $\Sigma F_y = 0$ just means N - N = 0, or N = N, which is already given. It might make more sense if the top one had been labeled N1 and bottom one N2. Anyway, they have to be equal to each other because there are no other forces in the y direction.

Now, take the x direction. $\Sigma F_x = 0$ just means that T - T = 0. Again, trivial in this problem. So, forget about summing forces because it's already done.

Now, for the moments. By the way, you are correct that the center of mass is where the 2 rollers touch. There are 4 moments acting at the center of mass. At the top you have N times it's 'lever arm' (don't know what terminology you use, T times its lever arm acting in the opposite direction as the first one. You also have the same situation at the bottom. Thus, all you have to do is calculate the lever arms based on the geometry, multiply those by the forces (keeping the CCW and CW directions correct), sum them, set the sum equal to zero, and solve for N (because T is expressed in terms of N). You have single equation in N.

If you aren't sure what I mean by 'lever arm', a moment is determined by multiplying a force by a distance that is perpendicular to the direction of the force and through the center of mass. In other words, the force and the lever arm are at right angles.

P.S. I hope your other post about nobody responding was referring to the 2nd problem, not this one.

OH! That makes sense! Thank you so much!

P.S. I hope your other post about nobody responding was referring to the 2nd problem, not this one.

And yeah...got any clues on that one? I THINK I may have calculated the moments on each wheel correctly (but very likely didn't), but then am really confused as to how to get their resultant--is the resultant about the axes origin? What about the resultant angles? Since nothing else is given but the 60deg. angle from the y-axis, I'm wondering just what to do--sum them somehow? Here it is again:
http://img347.imageshack.us/img347/2488/problem64sx.jpg

 

[Doc Al]

And yeah...got any clues on that one? I THINK I may have calculated the moments on each wheel correctly (but very likely didn't), but then am really confused as to how to get their resultant--is the resultant about the axes origin? What about the resultant angles? Since nothing else is given but the 60deg. angle from the y-axis, I'm wondering just what to do--sum them somehow? Here it is again:
http://img347.imageshack.us/img347/2488/problem64sx.jpg

Each couple produces a vector moment. (What is the direction of those moments?) Add those two vectors.

(And please don't post the same question in mutliple threads!)

 

[caddyguy109]

Each couple produces a vector moment. (What is the direction of those moments?) Add those two vectors.

(And please don't post the same question in mutliple threads!)

Sorry about that...a little late night hysteria

Thanks, I'll see where this all gets me.

 

[caddyguy109]

Okay, so for the first problem with the rollers, would the "lever" arm be the distance from point A to the center of the masses? Then point B to the center, etc.? I'm still a little confused on that one. Would the moments with N have a different r than the moments with T?

Like:
At top:
M1)=(-N)(r)
M2)=(-T)(r)

At bottom:
M3)=(N)(r)
M4)=(T)(r)

where r is the distance mentioned above, and then plugged in at the end when all the moments are summed? Do I need an angle for each?

 

[hotvette]

The r's aren't the same in both cases. Maybe this will help illustrate.

 

[caddyguy109]

Um, okay.

So the r for N forces would be:
0.025*cos(30)=0.029 and total d1=0.029*2=0.058

And the r for T forces would be:
0.025*sin(30)=0.0125 and total d2=0.0125*2=0.025

Right?

 

[caddyguy109]

Then combining them all, I'm getting a little confused again ( ):

M1=(N)(-d1/2)
M2=(T)(-d2/2)
M3=(N)(d1/2)
M4=(T)(d2/2)

Meq=M1+M2+M3+M4

But then if I combine them, the distances cancel out because of the signs...should they all be positive instead?

 

[caddyguy109]

If positive, then I get:
Meq=N(d1)+T(d2)
N(d1)=Meq-T(d2)
N=[-T(d2)]/2
N=-6.47N
but then [N]=[N] so N=6.47N

Or no?

 

[hotvette]

You got it, except signs. I believe I may have made things more complicated by talking about individual moments as opposed to the couple. The result is the same though. Take a look at the directions. The N's produce moments in the same direction, not oppisite. Meaning, they add. Same with the T's. You are almost there.

 

[hotvette]

I think you may have it. I won't check the math of determinining d1 and d2, though. You can check your answer by multiplying N x d1 and T x d2 and see if they are the same.

By the way, what I meant by added complication is that it's simpler to consider the effect of the couples as opposed to the individual moments:

(d1 x N) - (d2 x T) = 0, or d1 x N = d2 x T. You know T in terms of N, and you know d1 and d2, so you end up with a single equation in N.

P.S. I believe N = 6.47N means N = 6.47 Newtons? It's unfortunate that the symbol for Newtons is the same as the symbol used for the force - can be confusing.

 

[caddyguy109]

Ok, thanks again--that clarifies it more, and I think finishes it

Now got to finish the second one.
http://img347.imageshack.us/img347/2488/problem64sx.jpg
If I have this:
MA=(d)(F1)=(0.175m)(35k N)=6.125k Nm
MB=(d)(F2)=(0.175m)(25k N)=4.375k Nm

But the center of MB is angled 60deg. off the y-axis. So, when I add them, how do I factor that in?

Meq=MA+MB
Meq=(6.125k)i + (4.375k)j*cos(60)...?

 

[caddyguy109]

Anybody on this second problem?

 

[hotvette]

Doc Al said it:

Each couple produces a vector moment. (What is the direction of those moments?) Add those two vectors.

 

[caddyguy109]

Doc Al said it:

I get that, but if the actions of each wheel are in the z (or k) direction, how the heck do I apply the 60deg. from the y-axis part?

MA=(d)(F1)=(0.175m)(35N)=6.125(0i+0j+1k)Nm=(0i+0j+6.125k)Nm

MB=(d)(F2)=(0.175m)(25N)=4.375(0i+sin(60)j+1k)Nm=(0i+3.79j+4.375k)Nm

Like that? And then add them?

 

[Doc Al]

Not sure what you are doing with the angles. Both moments act in the x-y plane, so there shouldn't be any $\hat{k}$ involved. The first moment acts in the -x direction ($- \hat{i}$); the second moment is at a 60 degree angle to the x-axis (find the components of that vector: it will have both an x and a y component).

 

[caddyguy109]

...yeah, I realized that after I stared at it for a while.

Thanks again for ALL the help. My internet died around 2:30pm yesterday so I couldn't get back on at all until this morning, so I basically had to stare at it for a while, ask a few people--and am pretty sure I got it.