- #1
leospyder
- 9
- 0
I need to derive the formula for this "film projection wheel" (it just has four holes in the center). I've looked all over google AND Hyperphysics but I haven't found a site that shows how to derive the formulas.
Please can someone help me (my physics teacher is a dick: he's been missing for 3/4 of the semester).
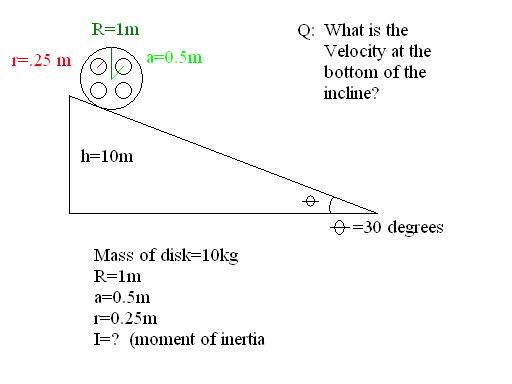
Please can someone help me (my physics teacher is a dick: he's been missing for 3/4 of the semester).