- #1
mirandasatterley
- 62
- 0
Homework Statement
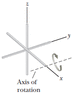
"Three identical thin rods, each of length L and mass m, are welded perpendicular to one another. The assembly is rotated about an axis that passes through the end of one rod and is parallel to anotther, determine the moment of inertia of this structure."
Homework Equations
I(for a long thin rod with a rotation axis through it's end) = 1/3 ML^2
The Attempt at a Solution
I(for the whole system) = I (rod 1) + I (rod 2) + I (rod 3)
For the rod where the rotation axis passes through the end of the rod, I'm thinking that its moment of inertia should be 1/3 ML^2.
For the rod which is parallel to the axis of rotation, I have been told by my prof that the monent of inertia is zero. Could someone breifly explain why this is.
For the last rod, I'm not sure what it moment of inertia is.
If any of this is right, please let me know and any other help is appreciated.