- #1
coldblood
- 133
- 0
Hi friends the problem is as:
https://fbcdn-sphotos-d-a.akamaihd.net/hphotos-ak-ash4/1379445_1440214886205617_1276077735_n.jpg
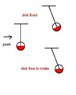
While finding moment of inertia of the system about the point from where the rod is fixed, the book says that M.I. of the system will be,
I = Irod + Idisc
I = [1/3m(2R)2] + [m(2R)2]-----------(1)
Sorry in the figure the length of the rod is 2R.
But I think that it should be
I = Irod + Idisc
I = [1/3m(2R)2] + [1/2m(R)2 + m(2R)2] - - - -- - (2)
(Using parallel axis theorem)
Please friends tell why it is so?
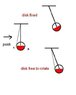
While the (2)nd M.I. which I got, the book says that it will be for,
https://fbcdn-sphotos-b-a.akamaihd.net/hphotos-ak-ash4/q71/1378467_1440214882872284_972543142_n.jpg
Please friend help me in this confusion. I will appreciate the help.
Thank you all in advance.
https://fbcdn-sphotos-d-a.akamaihd.net/hphotos-ak-ash4/1379445_1440214886205617_1276077735_n.jpg
While finding moment of inertia of the system about the point from where the rod is fixed, the book says that M.I. of the system will be,
I = Irod + Idisc
I = [1/3m(2R)2] + [m(2R)2]-----------(1)
Sorry in the figure the length of the rod is 2R.
But I think that it should be
I = Irod + Idisc
I = [1/3m(2R)2] + [1/2m(R)2 + m(2R)2] - - - -- - (2)
(Using parallel axis theorem)
Please friends tell why it is so?
While the (2)nd M.I. which I got, the book says that it will be for,
https://fbcdn-sphotos-b-a.akamaihd.net/hphotos-ak-ash4/q71/1378467_1440214882872284_972543142_n.jpg
Please friend help me in this confusion. I will appreciate the help.
Thank you all in advance.