- #1
dinospamoni
- 92
- 0
Homework Statement
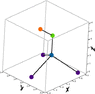
A molecule similar to methanol is made by joining three flourine atoms (purple; m = 19 amu each) to one carbon atom (blue; 12 amu) to one oxygen atom (green; 16 amu) to one potassium atom (orange; 39 amu). The position of each atom is as follows:
1. The flourine atoms are evenly spaced about the origin in the z = 0 plane, with one of them on the x-axis at -0.476 nm.
2. The carbon atom is on the z axis at z = 0.238 nm.
3. The oxygen atom is on the z axis at z = 0.952 nm.
4. The potassium atom is located at coordinates (x, y, z) = (-0.357, 0.000, 1.190) nm.
Determine the components of the inertia tensor for this molecule. Enter a) Ixx, b) Iyy, and c) Izz.
Picture is attached
Homework Equations
Ixx= ∫ y^2 + z^2 dm
Iyy= ∫ x^2 + z^2 dm
Izz= ∫ x^2 + y^2 dm
The Attempt at a Solution
I'm not sure where to start with this one. I've only ever had to find the moment of inertia for a solid object, never a collection of small objects. For those I converted to spherical coordinates and solved it that way.
I think the first thing that would help me out is finding out how to integrate over mass, or finding a substitute for it which would be easier to integrate over. Any suggestions?