- #1
barryj
- 854
- 51
Homework Statement
[/B]
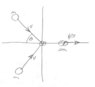
After a completely inelastic collision between two objects of equal mass, each having an initial speed of v, the two move off together with a speed of v/3. What is the angle between their initial directions.
Homework Equations
Conservation of momentum in both x and y directions.
The Attempt at a Solution
See the attached diagram.
Are my equations correct? if so how are they solved.
When plotted they do not cross.