What factors affect monochromator bandwidth?

[oskarbjo]

< Mentor Note -- thread moved to HH from the technical physics forums, so no HH Template is shown >

Hi!

I am having a bit trouble understanding how to determine the wavelength bandwidth for a monochromator. If anyone could suggest what to look for it'd be really nice. The problem is formulated something like this:

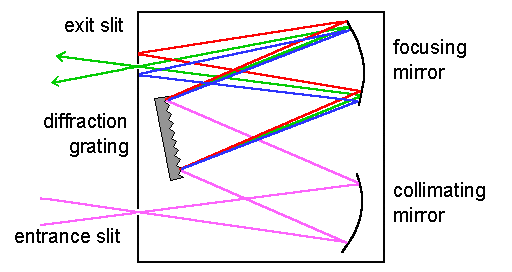
White light is aimed into a monochromator. The monochromator consists of a grating (with slit spacing d) that the light is reflected from. This light is then aimed to a slit with width t. How will the interval of wavelengths that comes out from the slit depend on t and d?

I don't see how this information is enough to determine the bandwidth. If anyone could give me a hint I'd be really thankful.

Edit: I missed there was a forum for homework. Requested thread to be moved

Oskar

 

[blue_leaf77]

First write out the diffraction grating equation for the parameters given.

 

[oskarbjo]

The grating equation goes like this:

d(sin a1 + sin a2) = m*lambda

Where a1 is the incident angle relative to the grating normal and a2 is the reflected angle, m is the diffraction order and d is the grating slit distance.
I understand that only a certain portion of the reflected spectrum will 'fit' through the exit slit, but what's made me get stuck is that I think that this portion, the bandwidth, will depend on the distance between the grating and the exit slit. The picture included in this post is the one that I got with the task (used another one in the first post because I thought it looked better and was in english). The only information I have is the grating slit distance d and the exit slit width t.

Vitt ljus = White light
Roberbart gitter med spaltavstånd d = Rotatable grating with slit distance d
Prov = Sample

 

[blue_leaf77]

So in the original problem there is no focusing mirror?

 

[oskarbjo]

You mean the focusing mirrors? No, nothing like that

 

[blue_leaf77]

Well, in that case then you do need to define the distance between grating and the exit slit. For the grating equation, usually the diffraction order used in separating the frequency components is the first order, $m=1$. Compute the diffracted angle as a function of wavelength with $m=1$ and you should obtain the answer.