- #1
stunner5000pt
- 1,461
- 2
of the classical kind
All i need here is an explanation as why F is the way it is
A person wished to fence off a maximum area for hi8s dog by attachin a flexible fence of length L to the side of his house whose width is 2a. What should the slope of the fence be?
Assume L > 2a
well then the action
[tex] A[y] = \int_{-a}^{a} y(x) dx [/tex] is a maximum
subject to constant L where [tex] L = \int_{-a}^{a} \sqrt{1+y'^2} dx [/tex]
If L[y,y'} = constant then [itex] \delta L = 0 [/itex]
and A[y,y'] = constant at its maximum
then
[tex] \delta A + \lambda \delta L = 0 [/tex] where
[tex] \lambda = \frac{[A]}{[L]} [/tex]
we also want that [tex] \delta \int_{-a}^{a} F(y,y',x) dx = 0 [/tex]
where [tex] F = y + \lambda \sqrt{1+y'^2} [/tex]
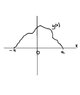
thats the problem, Why is F the way it is ? Maybe the attached diagram helps...
All i need here is an explanation as why F is the way it is
A person wished to fence off a maximum area for hi8s dog by attachin a flexible fence of length L to the side of his house whose width is 2a. What should the slope of the fence be?
Assume L > 2a
well then the action
[tex] A[y] = \int_{-a}^{a} y(x) dx [/tex] is a maximum
subject to constant L where [tex] L = \int_{-a}^{a} \sqrt{1+y'^2} dx [/tex]
If L[y,y'} = constant then [itex] \delta L = 0 [/itex]
and A[y,y'] = constant at its maximum
then
[tex] \delta A + \lambda \delta L = 0 [/tex] where
[tex] \lambda = \frac{[A]}{[L]} [/tex]
we also want that [tex] \delta \int_{-a}^{a} F(y,y',x) dx = 0 [/tex]
where [tex] F = y + \lambda \sqrt{1+y'^2} [/tex]
thats the problem, Why is F the way it is ? Maybe the attached diagram helps...
Attachments
Last edited: