- #1
quickclick330
- 83
- 0
[SOLVED] More trig substitution help...
I've looked at this problem about 3 times and still can't figure it out...where identity did they use to substitute out the part in the red box? Thanks for the help
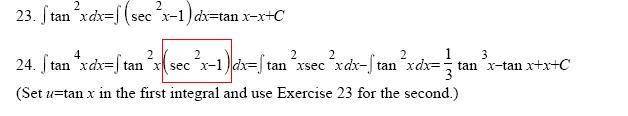
I've looked at this problem about 3 times and still can't figure it out...where identity did they use to substitute out the part in the red box? Thanks for the help