Motion in a Magnetic Field 2

[Gee Wiz]

Homework Statement

A proton (q = 1.6 X 10-19 C, m = 1.67 X 10-27 kg) moving with constant velocity enters a region containing a constant magnetic field that is directed along the z-axis at (x,y) = (0,0) as shown. The magnetic field extends for a distance D = 0.64 m in the x-direction. The proton leaves the field having a velocity vector (vx, vy) = (2.2 X e5 m/s, 0.9 X e5 m/s).

What is R, the radius of curvature of the motion of the proton while it is in the region containing the magnetic field?

Homework Equations

F=qv*b
m*(v^2)/R=F

The Attempt at a Solution

Well, I first wanted to try to find theta. So i did arctan(.9e5/2.2e5). Then using that angle i did .64 (my dimension D) divided by sin of that angle. Which gives me the correct radius. Yet, when i look at the trig behind this is does not make sense to me. I would think i should use cos of the angle, but that is incorrect.

https://www.smartphysics.com/Content/Media/Images/EM/12/h12_bendtheta.png

 

[TSny]

Hi Gee Wiz.

You probably new this was coming
Please explain why you think you should use cosine?

 

[Gee Wiz]

alright well, because cosine is adjacent over hypotenuse. I assumed (perhaps incorrectly) that the angle i found from the velocity would the the angle that the radius and D would create. So, therefore D is adjacent to the angle.

 

[TSny]

I assumed (perhaps incorrectly) that the angle i found from the velocity would [be] the angle that the radius and D would create. So, therefore D is adjacent to the angle.

The radius that goes through the point where the particle exits the square does not make an angle with respect to the horizontal that is equal to the angle that the velocity makes to the horizontal. Did you construct a diagram to check your assumption?

 

[Gee Wiz]

I tried to draw a diagram, but it didn't really look right to me. Since the, i guess the vertical direction is not a straight line, but rather a curve.

 

[TSny]

I'm not following your comment. Let's first make sure we're clear on some basics. Can you describe the general shape of the path of the particle as it moves in the magnetic field?

 

[Gee Wiz]

Well, a particle in a magnetic field would follow a circular path.

 

[TSny]

Ok. How is the direction of the velocity vector of the particle related to the circular path?

 

[Gee Wiz]

The velocity vector is tangential to the path and perpendicular to the force vector

 

[TSny]

Good. Can you tell roughly where the center of the circle will be? Will it be somewhere on the y-axis? The x-axis? Neither?

 

[Gee Wiz]

I believe the center would be at the origin?

 

[TSny]

Well, the particle passes through the origin. So, are you saying that the particle passes through the center of the circle that it travels on?

 

[Gee Wiz]

Ahh, okay so perhaps that's my issue. I was kind of imagining the square was containing a fourth of a circle centered at the origin. But, now I'm kind of thinking that the center of this circle would be (.32,.32)

 

[TSny]

Let's see. Consider the instant when the particle is at the origin and moving horizontally to the right. We know the velocity is tangent to the circle. So, that means the velocity is perpendicular to the radius. So, if the velocity is horizontal at the origin, what would be the direction of the radius of the circle at that point?

 

[Gee Wiz]

In the positive y direction

 

[TSny]

Yes. So, does that help to see roughly where the center of the circle would be?

 

[Gee Wiz]

Above (direction of the positive y axis) the square. Would it be centered at x=0, and some y value..1.69(since that's the radius i magically stumbled upon)?

 

[TSny]

Right, the center will be somewhere on the y-axis. To get a better idea of the location of the center on the y-axis, go to the point where the particle leaves the blue square and the velocity is tilted up at the angle θ. Can you draw the direction of the radius at this point?

 

[Gee Wiz]

I think i would go from the point where the particle leaves the blue square and go up at some angle to the y-axis. The x-direction or component would be d, would this then make the angle that the y-axis and the radius to the point make the same angle as the one at the velocity vector? (yes, i realize that is wordy. my apologies)

 

[TSny]

Yes, that's right. The radius is always perpendicular to the velocity. So, if the velocity makes angle θ to the horizontal, then the radius will make the same angle θ with respect to the vertical.

 

[Gee Wiz]

okay, so then the center of the circle would be at (0,1.69+h)?

 

[TSny]

No. If you go back to where the particle is at the origin, how far up the y-axis would you need to go to reach the center of the circle? That is, how far is it from a point on the circle to the center of the circle?

 

[rude man]

I will leave it to others to approach this via vector components, etc. I'm curious myself.

This could however also be done strictly geometrically: define the circle, the arc of which runs from (0,0) to (D,h). General expresssion for a circle is (x-x0)^2 + (y-y0)^2 = R^2.

You have 2 points to substiture for x and y so can write 2 equations in x0, y0 and R. You also have a third equation which is dy/dx at (D,h). That theoretically let's you solve for x0, y0 and of course R.

Realize that the magnitude of v does not change. Why?

 

[Gee Wiz]

Opps. I mistook the hypotenuse to be the same as the vertical component. I would have to do 1.69*cos(angle that was found). to get the height plus h

 

[Gee Wiz]

although, i could also just say that the height is just 1.69 right? Since the velocity vector is perpendicular to the radius

 

[TSny]

Yes, the center of the circle will just be up the y-axis from the origin a distance of the radius of the circle. The important thing is to see how to get the radius R from the given information. Hopefully, the attached picture is similar to your drawing.

 

[Gee Wiz]

Yes, that is what i drew. Although it looks better computer drawn then my artistic attempt lol. This makes a lot more sense now. Thank you again for your thorough explanations. I find them very helpful. It is nice to be able to talk/type through my thought process to expose its faults.

 

[TSny]

This could however also be done strictly geometrically: define the circle, the arc of which runs from (0,0) to (D,h). General expresssion for a circle is (x-x0)^2 + (y-y0)^2 = R^2.

You have 2 points to substiture for x and y so can write 2 equations in x0, y0 and R. You also have a third equation which is dy/dx at (D,h). That theoretically let's you solve for x0, y0 and of course R.

That should work. The algebra would be a little tedious.

 

[rude man]

That should work. The algebra would be a little tedious.

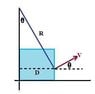
Agreed. The (obvious) point I didn't think of is that R is perpendicular to v all along the B trajectory including at (D,h). Very nice.