- #1
andyrk
- 658
- 5
Suppose a lift is moving in a shaft upwards with a velocity a. Then why does the net acceleration of the lift become (a+g)? Life suppose a liquid of denisty ρ is kept at rest in a beaker. In this case as pressure changes only in horizontal direction so we can write:
dP/dx=0 and dP/dy=-ρg
But, soppose the beaker is accelerated and it has components of acceleration ax and ay in the x and y directions respectively, the above above equations in this case reduce to
dP/dx=-ρax
dP/dy=-p(g+ay)
Why does addition of accelerations in the y-direction happen? Shouldn't we subtract g from ay as both of them are in opposite directions?
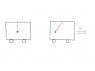
I am posting two attachments. First one is for an accelerating cart with a bob hanging inside it.
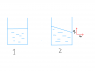
Second is for an accelerating beaker with liquid inside it. I want to know why does the liquid incline from top left to down bottom when we accelerate the beaker towards the right. Is it analogous to cart situation in any way? If yes then how?
dP/dx=0 and dP/dy=-ρg
But, soppose the beaker is accelerated and it has components of acceleration ax and ay in the x and y directions respectively, the above above equations in this case reduce to
dP/dx=-ρax
dP/dy=-p(g+ay)
Why does addition of accelerations in the y-direction happen? Shouldn't we subtract g from ay as both of them are in opposite directions?
I am posting two attachments. First one is for an accelerating cart with a bob hanging inside it.
Second is for an accelerating beaker with liquid inside it. I want to know why does the liquid incline from top left to down bottom when we accelerate the beaker towards the right. Is it analogous to cart situation in any way? If yes then how?
Attachments
Last edited: