- #1
compaq65
- 17
- 9
- Homework Statement
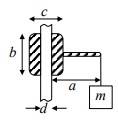
- There is a rod with a nut on it. Diameter of rod is d. There is a mass m object as shown in picture. all other parameters (a, b, c) are known. What coefficient of friction should be, so that nut is not moving.
- Relevant Equations
- Sum of moments and Newton I law.
I tried to draw a free-body diagram and sum of moments equal to zero, but I stuck there, because I don't know where should reaction force N be and how determine where friction is acting on round surface? Any ideas?