- #1
PhizKid
- 477
- 1
Multiloop circuit/Kirchhoff
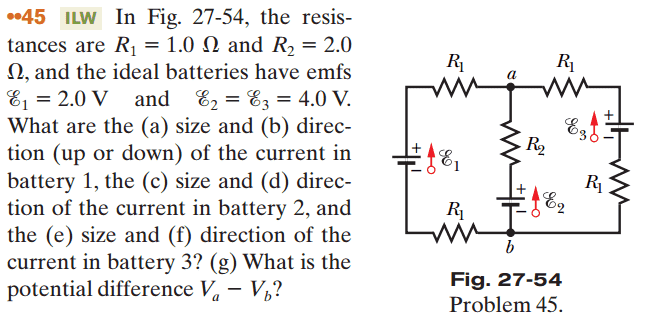
Kirchhoff's rules
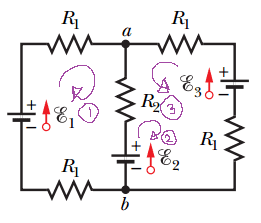
These are the 3 paths I decided to take (at random):
So for the first battery, I get:
##2V - 1i_1 - 2i_1 - 4V - 1i_1 = 0##
## -4i_1 = 2V##
## i_1 = -\frac{1}{2}##
2nd:
##4V - 2i_2 - 1i_2 - 4V - 1i_2 = 0##
##- 2i_2 - 1i_2 - 1i_2 = 0##
##- 4i_2 = 0##
##i_2 = 0##
3rd:
##4V - 1i_3 - 2i_3 - 4V - 1i_3 = 0##
##- 1i_3 - 2i_3 - 1i_3 = 0##
##- 4i_3 = 0##
##i_3 = 0##
But these answers are wrong. What did I do incorrectly?
Homework Statement
Homework Equations
Kirchhoff's rules
The Attempt at a Solution
These are the 3 paths I decided to take (at random):
So for the first battery, I get:
##2V - 1i_1 - 2i_1 - 4V - 1i_1 = 0##
## -4i_1 = 2V##
## i_1 = -\frac{1}{2}##
2nd:
##4V - 2i_2 - 1i_2 - 4V - 1i_2 = 0##
##- 2i_2 - 1i_2 - 1i_2 = 0##
##- 4i_2 = 0##
##i_2 = 0##
3rd:
##4V - 1i_3 - 2i_3 - 4V - 1i_3 = 0##
##- 1i_3 - 2i_3 - 1i_3 = 0##
##- 4i_3 = 0##
##i_3 = 0##
But these answers are wrong. What did I do incorrectly?
Last edited:

