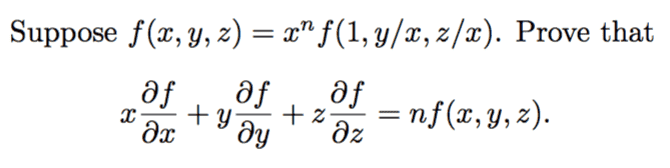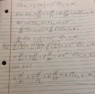Need help with a calculus III proof

[dakota1234]

I've been working on this one for a little bit, and I know I really just need to use the chain rule to solve it, but I can't seem to figure out how to set it up properly. Probably a dumb question, but I could really use some help on this!

 

[dakota1234]

I was able to work out a more generalized version of the proof, but I'm not sure how to apply it

 

[Delta2]

you are given that $f(x,y,z)=x^nf(1,y/x,z/x)$ (1). If from (1) you can prove that $f(tx,ty,tz)=t^nf(x,y,z)$ (2) then together with the work already done by you , you ll be finished.

Now if you apply (1) for $x=tx,y=ty,z=tz$ what do you get? if you apply it correctly you ll get a result that if you apply (1) again (as it is directly, without substitution) you ll be able to prove (2).

 

[dakota1234]

you are given that $f(x,y,z)=x^nf(1,y/x,z/x)$ (1). If from (1) you can prove that $f(tx,ty,tz)=t^nf(x,y,z)$ (2) then together with the work already done by you , you ll be finished.

Now if you apply (1) for $x=tx,y=ty,z=tz$ what do you get? if you apply it correctly you ll get a result that if you apply (1) again (as it is directly, without substitution) you ll be able to prove (2).

I may just be really tired, but can you explain in more detail how "to apply it correctly"? I've tried plugging in the substitutions for x,y,z, since before I even posted on this forum, and I don't understand what I'm doing wrong.

 

[Delta2]

Ok, let's say that $f(u,v,w)=u^nf(1,v/u,w/u)$ (1)

Applying (1) for $u=tx,v=ty,w=tz$ we get that $f(tx,ty,tz)=(tx)^nf(1,\frac{ty}{tx},\frac{tz}{tx})=t^nx^nf(1,y/x,z/x)$

Now i have helped too much i think you must be able to see the last step, what is $x^nf(1,y/x,z/x)$ equal to?