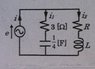
- #1
MissP.25_5
- 331
- 0
i1(t) = √2sin(2t+2π/3) [A]
i2(t) = √2sin(2t+π/6) [A]
1. Find R and L.
2. Given that the phase difference between e and i is arg(e/i)=θ. Find tan θ.I am not sure how to do this. I know that first we need to find e. Is it easier to use phasors to solve this or solve it in time function form? Did I get the e correct?
i2(t) = √2sin(2t+π/6) [A]
1. Find R and L.
2. Given that the phase difference between e and i is arg(e/i)=θ. Find tan θ.I am not sure how to do this. I know that first we need to find e. Is it easier to use phasors to solve this or solve it in time function form? Did I get the e correct?
Attachments
Last edited: