Need some help with spring-mass-damper problem

[foster182]

I know some people might find this a stupid question but

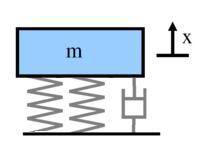
What effect would the addition of

1)additional springs
2)additional dampers

have on vibration absorption properties?

In plain English please, I’m only learning

thanks guys

 

[Kurdt]

Welcome to the forums foster182!

It is the policy of this forum that the poster has shown some attempt at doing the problem themselves. What do you think would happen in both the scenarios described?

 

[foster182]

well with the increase of a damper or additional spring it would absorb more vibration thus coming to a steady state. yes?

how would i derive an equation from that?

 

[Kurdt]

Well the addition of more springs (I assume they will be added in parallel from the diagram) will give the system an effective spring constant which is the sum of the spring constants of all the springs. What effect would that have on the system if the damping was kept the same?

 

[foster182]

sorry i should of made that more clear

and with additional damper and spring

the system will react differantly when i add the damper and spring separate than together etc, but i don't know how to derive an expression from it.

 

[Kurdt]

Oh so that picture was of the new system. Got it. Well like I said before the spring constant will be the sum of the spring constants of the two springs. What effect will that have of the vibration of this system? Now its also damped, what do you know of damping of oscillations?

Consider a cars suspension and what it has to do to make the ride bearable.

 

[foster182]

o.k. i think i have it now,
so in the case of me adding the damper to the existing spring

net force applied to ( mass m= F - kx - cv )

then to model that ( m d2x/dt2 = F- kx - c dx/dt ) taken v as velocity

something like that?

sorry i don't know much about damping of oscillations? i will read up on it.

 

[Kurdt]

Yeah, you're almost there:

$$m\frac{d^2x}{dt^2}+c\frac{dx}{dt}+kx=0$$

is probably the standard form.

That of course does assume certain things about the damping force that means it can be approximated as linear.

 

[foster182]

yes it would be linear,
and if i was to add another spring

m d2x/dt2 + c dx/dt + kx(2) = F

if the two springs have the same resistance

yes?

if not?

 

[Kurdt]

Like I mentioned before the spring constants add together to give and effective spring constant.

$$m\frac{d^2x}{dt^2}+c\frac{dx}{dt}+(k_1+k_2)x=0$$

 

[foster182]

ah i see thank you!